Concetti Chiave
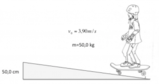
- Un flacone di detersivo viene lasciato scivolare con velocità iniziale di 1,1 m/s dal bordo di una vasca.
- La velocità del flacone al fondo della vasca è di 3,1 m/s, considerato il livello zero di energia potenziale.
- L'energia potenziale iniziale del flacone viene calcolata come lavoro, pari a 6,3 J.
- La variazione di energia cinetica permette di calcolare il lavoro fatto dal flacone durante la discesa.
- L'altezza della vasca viene determinata utilizzando la formula dell'energia potenziale gravitazionale, risultando 0,43 m.
Un flacone di detersivo di massa
scivola dal bordo di una vasca da bagno con velocità iniziale di
fino a raggiungere il fondo della vasca, scelto come livello zero, a una velocità di
.
- Calcola l'altezza della vasca. (L'effetto dell'attrito è trascurabile).
Svolgimento
Per poter calcolare l'altezza della vasca, dobbiamo conoscere l'energia potenziale gravitazionale che possiede il flacone al momento iniziale.
Sappiamo che il lavoro corrisponde alla variazione negativa dell'energia potenziale, cioè:
Sapendo che è stato assunto come livello zero dell'energia potenziale il fondo della vasca, sappiamo che l'energia potenziale finale è uguale a zero, quindi:
Possiamo calcolare il lavoro sapendo che esso è uguale alla variazione di energia cinetica:
Sostituiamo quindi i valori numerici:
Quindi, poiché il lavoro è uguale all'energia potenziale iniziale, sappiamo che:
Sapendo che:
possiamo ricavare l'altezza con la formula inversa:
Troviamo quindi il valore dell'altezza della vasca:
Accedi a tutti gli appunti
Tutor AI: studia meglio e in meno tempo
