Concetti Chiave
- La frequenza del disco è calcolata come 0,75 Hz, derivata da 135 giri in 3 minuti.
- Il periodo di rotazione è di 1,33 secondi, calcolato come l'inverso della frequenza.
- Il raggio della circonferenza è determinato come 8,44 cm usando la formula inversa della circonferenza.
- La velocità lineare di un punto sul bordo del disco è 39,8 cm/s.
- La velocità è convertita in unità standard, risultando in 0,398 m/s.
[math]53 cm[/math]
e contiene una canzone di durata pari a [math]3.0 min[/math]
. Per ascoltarla, il disco deve compiere [math]135[/math]
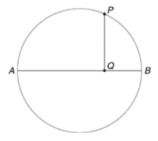
giri.- Calcola il modulo della velocità di un punto che si trova sul bordo della circonferenza.
Svolgimento
La velocità, nel moto circolare uniforme, è data dalla formula[math] v = \frac{2 \pi r}{T} [/math]
, mentre il periodo ( [math]T[/math]
), dalla formula [math]T = \frac{1}{F}[/math]
.Per prima cosa, quindi, troviamo la frequenza che per definizione è il numero di oscillazioni completa effettuate in un secondo.
Poiché il disco compie
[math]135[/math]
giri in [math]3[/math]
minuti, possiamo ricavare il numero di giri in un secondo:
[math] \frac{g}{min} = \frac{135}{3} = 45 g/(min) [/math]
[math] F = \frac{45}{60 s} = 0,75 s^{-1} = 0,75 Hz [/math]
Ricaviamo quindi il periodo:
[math] T = \frac{1}{F} = \frac{1}{0,75 s^{-1}} = 1,33 s [/math]
Per trovare la velocità è necessario conoscere il raggio della circonferenza.
Il problema fornisce la lunghezza della circonferenza, possiamo quindi trovare il raggio dalla formula inversa:
[math] C = 2 \pi r \to r = \frac{C}{2 \pi} = \frac{53 cm}{2 \cdot 3,14} = 8,44 cm [/math]
A questo puto possiamo trovare la velocità :
[math] v = \frac{2 \pi r}{T} = \frac{2 \cdot 3,14 \cdot 8,44 cm}{1,33 s} = \frac{53 cm}{1,33 s} = 39,8 (cm)/s [/math]
Trasformiamo ora la velocità in m/s:
[math] v = 39,8 (cm)/s = 39,8 \cdot \frac{10^{-2}}{s} = 0,398 m/s [/math]
Accedi a tutti gli appunti
Tutor AI: studia meglio e in meno tempo
