Concetti Chiave
- La forza di attrito che agisce sulla cassa è di 23N, calcolata come la componente parallela del peso.
- L'angolo del piano inclinato è di 30°, determinato utilizzando il seno dell'angolo rispetto alle dimensioni del piano.
- La reazione normale del piano è 40N, ottenuta come la componente perpendicolare del peso.
- Il coefficiente di attrito statico è 0,58, calcolato dividendo la forza di attrito per la reazione normale.
Ricordiamo che quando l'attrito statico impedisce lo scivolamento di un corpo vale la relazione:
[math] \vec{F_{//}} = -\vec{F_s} [/math]
In particolare la forza di attrito statico ha un valore massimo che è dato da:
[math] \vec{F_{s max}} = \vec{F_{\perp}} \cdot \mu_s [/math]
[math] \mu_s [/math]
coefficiente di attrito statico. Vediamo ora il testo di un esercizio.
Testo dell'esercizio
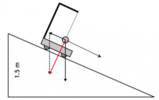
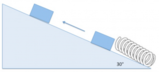
In un negozio di frutta e verdura una cassa di mele è appoggiata su un piano inclinato alto 50cm e lungo 1,0m. La cassa, che pesa 46N, è tenuta in equilibrio dalla forza di attrito statico.Qual è l' intensità della forza di attrito che agisce sulla cassa?
Qual è l' intensità della reazione normale del piano?
Quanto vale il coefficiente di attrito statico?
Svolgimento dell'esercizio
La forza di attrito deve essere uguale alla componente parallela del peso:[math] F= P \cdot \sin \alpha= P \cdot \frac{h}{l} = 46N \cdot \frac{0.5 m}{1.0 m} = 23N[/math]
La reazione normale del piano sarà invece uguale alla componente perpendicolare del peso:
[math]N= P \cdot \cos \alpha= 46N \cdot \cos 30°= 40N[/math]
[math]\mu= \frac{F}{P}= \frac{23 N}{40 N} \sim 0.58[/math]
Accedi a tutti gli appunti
Tutor AI: studia meglio e in meno tempo
