Concetti Chiave
- Le grandezze fisiche si dividono in scalari e vettoriali, con le vettoriali che richiedono direzione e verso per essere definite.
- La velocità è una grandezza vettoriale, necessitando di modulo, direzione e verso per essere completamente determinata.
- I vettori possono essere scomposti in componenti orizzontali e verticali usando formule trigonometriche con angoli rispetto agli assi cartesiani.
-
Nel caso di un aereo in decollo inclinato a 15°, la componente verticale della velocità si calcola usando la formula:
v_y = v \cdot \sin(\theta). - Per un aereo a 600 km/h inclinato di 15°, la velocità verticale risultante è di circa 155 km/h.
In fisica esistono due tipi di grandezze: le grandezze scalari e le grandezze vettoriali. La velocità è una di queste ultime: infatti, basta pensare che la frase sto viaggiando a 2 m/s non ha "significato". La velocità non è univocamente determinata dal suo modulo, bisogna tenere conto anche di direzione e verso. In virtù di ciò i vettori sono solitamente inclinati di un certo angolo
[math] \theta [/math]
rispetto agli assi che vengono comunemente utilizzati.Dato un vettore
[math] \vec{v} [/math]
vale in generale infatti:[math] v_x = |\vec{v}| \cos (\theta) [/math]
[math] v_y = |\vec{v}| \sin (\theta) [/math]
[math] v_x, v_y [/math]
rappresentano rispettivamente la componente orizzontale e verticale del vettore [math] \vec{v} [/math]
lungo i due assi (tipicamente cartesiani e quindi ortogonali tra loro).Nel seguente esercizio applicheremo una di queste formule. Vediamo il testo:
Testo dell'esercizio
Durante la fase di decollo un aeroplano si stacca dal suolo con una velocità di 600 Km/h , stando inclinato di 15° rispetto alla pista orizzontale. Con quale velocità l' aereo si innalza verticalmente?
Svolgimento dell'esercizio
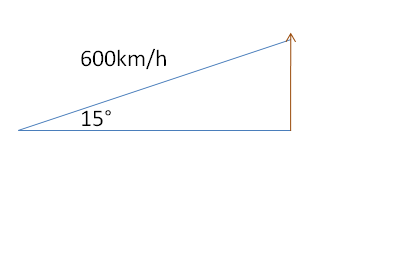
La componente verticale della velocità è quella evidenziata in rosso in figura, da cui si trova:
[math] v_y = v \cdot \sin(15^{\circ} ) [/math]
[math] v_y = 600 km/h \cdot \sin(15^{\circ}) \approx 155 km/h [/math]
Accedi a tutti gli appunti
Tutor AI: studia meglio e in meno tempo
