Gabbia e pappagallo

fabio.scardia
di fabio.scardia
1 min
Ominide
Vota
Appunto verificato
Contenuto verificato e approvato dal  Team di Esperti di Skuola.net Informazioni appunto verificato Informazioni appunto verificato hover

Scopri come calcolare la tensione di un cavo e la reazione di una sbarra in un sistema di forze. Analizziamo un esercizio pratico con una gabbia e un pappagallo, applicando le funzioni goniometriche e il Teorema di Pitagora per risolvere il problema.

Concetti Chiave

  • Scegliere un sistema di riferimento adeguato, con assi verticali e orizzontali, è fondamentale per semplificare i calcoli delle forze.
  • La tensione del cavo può essere calcolata utilizzando le funzioni goniometriche, considerando l'equilibrio delle forze verticali.
  • Nel caso dell'esercizio, la tensione del cavo è stata determinata come 200 N attraverso la formula T = P/sin(30°).
  • La forza vincolare della sbarra è orizzontale e viene calcolata in base alla componente orizzontale della tensione, risultando circa 173 N.
  • È possibile utilizzare il Teorema di Pitagora per calcolare la reazione vincolare, sfruttando la geometria del triangolo rettangolo formato dalle forze.

Quando si affrontano problemi come il seguente, ovvero problemi che richiedono il calcolo di più forze in una situazione in cui ne agiscono molteplici, è bene ricordare i seguenti fatti utili:

  • scegliere un sistema di riferimento comodo (tipicamente asse verticale e asse orizzontale);
  • calcolare correttamente utilizzando le funzioni goniometriche le varie componenti delle forze agenti lungo gli assi del sistema di riferimento.
Vediamo un esercizio di esempio.

Indice

  1. Testo dell'esercizio
  2. Svolgimento dell'esercizio

Testo dell'esercizio

All' estremità libera di un cavo, fissato a una parete verticale, è appesa una gabbia. La gabbia e il pappagallo pesano 100N complessivamente. Il cavo è appoggiato all' estremità di una sbarra incastrata nella stessa parete. Determina le intensità della tensione del cavo e della forza vincolare della sbarra.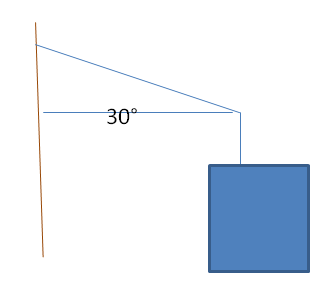 pappagallo.png

Svolgimento dell'esercizio

La tensione del filo è calcolabile, vale infatti essendo la gabbia in equilibrio che la somma delle forze applicate sull'asse verticale è nulla.
Dunque:
[math] T \sin (30°) = P \to T = \frac{P}{\sin (30°)} = \frac{100 N}{0.5} = 200 N [/math]
La reazione vincolare della sbarra è invece orizzontale, ed è bilanciata solo dalla componente orizzontale della tensione poiché il peso è verticale e quindi non ha componente orizzontale. Detta
[math] R [/math]
la reazione vale:
[math] T \cos(30°) = R \to R = 200 \cos(30°) \sim 173 N [/math]
In alternativa era possibile calcolare la reazione utilizzando il Teorema di Pitagora opportunamente, visto che la reazione cercata era uno dei cateti di un triangolo rettangolo di ipotenusa e primo cateto noti.

Domande da interrogazione

  1. Qual è l'importanza di scegliere un sistema di riferimento adeguato nei problemi di forze?

    2. Scegliere un sistema di riferimento comodo, tipicamente con un asse verticale e uno orizzontale, è fondamentale per semplificare il calcolo delle forze e delle loro componenti, come indicato nel testo.

  2. Come si calcola la tensione del cavo in un problema di equilibrio?

    3. La tensione del cavo si calcola utilizzando la relazione tra la tensione e il peso della gabbia, applicando le funzioni goniometriche. Nel caso specifico, si ha che \( T = \frac{P}{\sin(30°)} = 200 N \).

  3. Qual è il metodo alternativo per calcolare la reazione vincolare della sbarra?

    4. Un metodo alternativo per calcolare la reazione vincolare consiste nell'utilizzare il Teorema di Pitagora, poiché la reazione è uno dei cateti di un triangolo rettangolo con l'ipotenusa e un cateto noti, come descritto nel testo.

Appunti correlati

Domande e risposte

Hai bisogno di aiuto?
Chiedi alla community
Vai al forum