Concetti Chiave
- L'equilibrio su un piano inclinato non si verifica in assenza di attrito, poiché la forza peso agisce attraverso la sua componente parallela.
- La componente parallela della forza peso si calcola come
F_{//} = F_P \cdot \sin (\alpha), dove\alphaè l'angolo del piano inclinato. - È possibile determinare l'angolo di inclinazione usando la trigonometria e i dati disponibili, come la lunghezza e l'altezza del piano.
- Il coseno e il seno degli angoli in un triangolo rettangolo si calcolano usando i rapporti tra i lati dell'ipotenusa e dei cateti.
- Nel caso specifico di un esercizio, si calcola il peso della scatola utilizzando la relazione tra la forza parallela e il seno dell'angolo.
Quando si parla di equilibrio su un piano inclinato, è importante dire che in assenza di attrito esso, chiaramente, non può verificarsi. In effetti agisce sul corpo giacente sul piano inclinato la forza peso, sebbene essa non agisca direttamente. Risulta infatti più corretto parlare di componente parallela della forza peso, la quale fa sì che il corpo scivoli lungo il piano inclinato.
Tale forza soddisfa la relazione:
[math] F_{//} = F_P \cdot \sin (\alpha) [/math]
[math] \alpha [/math]
è l'angolo di inclinazione del piano inclinato e [math] F_P [/math]
è la forza peso.Ovviamente l'angolo di inclinazione del piano inclinato potrebbe non essere specificato subito in maniera chiara, ma è sempre possibile trovarlo in qualche modo con i dati a disposizione, come nell'esercizio precedente.
Basta usare opportunamente la trigonometria, ricordando che, fissato un triangolo rettangolo di una certa ipotenusa, il cateto adiacente si ottiene moltiplicando la lunghezza dell'ipotenusa per il coseno dell'angolo adiacente.
Analogamente, il cateto opposto si ottiene moltiplicando la lunghezza dell'ipotenusa per il seno dell'angolo adiacente.
Riarrangiando tali formule è possibile esprimere direttamente il coseno o il seno di tali angoli tramite i rapporti tra i lati, come vedremo nell'esercizio successivo.
Testo dell'esercizio
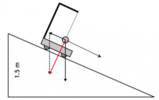
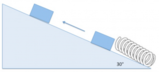
Per tenere in equilibrio una scatola di cioccolatini su un piano inclinato liscio lungo 50,0cm e alto 22,5cm occorre una forza di 3,97N. Ricava il peso della scatola.
Svolgimento dell'esercizio
Il peso lo otteniamo nel seguente modo:[math] P = \frac{F_{//}}{\sin A} \to P = \frac{F_{//}}{(h/l)} = \frac{3.97 N}{22.5/50} = 8.82 N [/math]
Accedi a tutti gli appunti
Tutor AI: studia meglio e in meno tempo
