Concetti Chiave
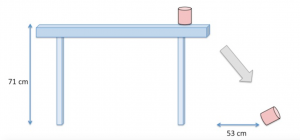
- La cameriera lancia un bicchiere vuoto orizzontalmente, che cade a terra a 53 cm dal bordo del tavolo.
- L'altezza del tavolo è di 71 cm, influenzando il tempo di caduta del bicchiere.
- La velocità iniziale del bicchiere al momento del distacco dal tavolo è calcolata come 1,4 m/s.
- La caduta del bicchiere a terra avviene in un tempo di 0,38 secondi.
- La traiettoria del bicchiere segue una parabola a causa della caduta libera, con velocità iniziale orizzontale.
In questo appunto analizzeremo un esercizio relativo al moto parabolico, caratterizzato dalla somma di due moti: uno orizzontale e uno verticale. Quello verticale è dovuto solitamente all'accelerazione di gravità mentre quello orizzontale da una sollecitazione esterna. Vediamo il testo dell'esercizio.
Testo dell'esercizio
Una cameriera distratta lancia orizzontalmente un bicchiere vuoto sul tavolo al barman perché lo riempia. Purtroppo il lancio è lungo, e il bicchiere cade a terra a una distanza orizzontale di[math]53 cm[/math]
dal bordo del tavolo che è alto [math]71 cm[/math]
. Calcola:- La velocità del bicchiere al momento del distacco dal tavolo;
- Dopo quanto tempo il bicchiere arriva a terra;
Svolgimento dell'esercizio
Calcoliamo la velocità con cui il bicchiere arriva al bordo del tavolo, un momento prima di cadere; per farlo, ricordiamo che la traiettoria descritta dal bicchiere in caduta libera è una parabola (con vertice nell'origine degli assi) , e, poiché la velocità iniziale è orizzontale, possiamo sfruttare l'equazione cartesiana della traiettoria seguita dal bicchiere:
[math] y = \frac{1}{2} \cdot \frac{g}{v_0 ^2} \cdot x^2 [/math]
dove
[math]x[/math]
e [math]y[/math]
sono le distanze (orizzontali e verticali) dal punto di partenza, [math]g[/math]
è l'accelerazione di gravità, mentre [math]v_0[/math]
è la velocità che stiamo cercando; ricaviamo quindi dall'equazione la velocità:[math] 2 \cdot v_0 ^2 \cdot y = g \cdot x^2 \to v_0 ^2 = \frac{g \cdot x^2}{2 \cdot y} [/math]
[math] v_0 = \sqrt{\frac(g \cdot x^2)(2 \cdot y)} [/math]
[math] x = 53 cm = 0,53 m [/math]
[math] x = 71 cm = 0,71 m [/math]
[math] v_0 = \sqrt{\frac{9,8 m/s^2 \cdot (0,53 m)^2}{2 \cdot 0,71 m}} = 1,392 m/s = 1,4 m/s [/math]
Possiamo ora calcolare dopo quanto tempo il bicchiere raggiunge il suolo:
[math] s = v_0 \cdot t \to t = \frac{s}{v_0} [/math]
[math] t = \frac{s}{v_0} = \frac{0,53 m}{1,4 m/s} = 0,38 s [/math]
Domande da interrogazione
- Qual è la velocità del bicchiere al momento del distacco dal tavolo?
- Dopo quanto tempo il bicchiere arriva a terra?
- Quali sono le equazioni utilizzate per calcolare la velocità e il tempo di caduta del bicchiere?
La velocità del bicchiere al momento del distacco dal tavolo è di 1,4 m/s.
Il bicchiere arriva a terra dopo 0,38 secondi.
Per calcolare la velocità è stata utilizzata l'equazione [math] v_0 = \sqrt{\frac{g \cdot x^2}{2 \cdot y}} [/math], mentre per il tempo di caduta è stata usata [math] t = \frac{s}{v_0} [/math].
Accedi a tutti gli appunti
Tutor AI: studia meglio e in meno tempo
