Concetti Chiave
- Una particella con carica +7,2 × 10-5 C e massa 10 g si muove in un campo elettrico uniforme tra due punti distanti 10 m con una differenza di potenziale di 24 × 103 V.
- Per calcolare il tempo di percorrenza della particella, si uguagliano le forze elettrica e dinamica per trovare l'accelerazione.
- L'accelerazione è espressa come a = (E · q) / m, dove E è il campo elettrico calcolato dalla differenza di potenziale e spostamento.
- Calcolando l'accelerazione, si ottiene a = 17,28 m/s2.
- Il tempo di percorrenza è determinato con la formula del moto uniformemente accelerato, risultando in t ≈ 1,1 s.
In questo appunto andremo a vedere un esercizio riguardante il campo elettrico applicato ad una particella.
Indice
Testo del problema
Una particella con carica elettrica
Svolgimento
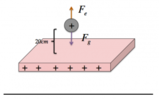
La particella in questione si trova all'interno di un campo elettrico, ed è quindi sottoposta alla forza elettrica del campo.Avendo anche una massa, è sottoposta anche alla forza
Per trovare il tempo impiegato dalla particella a percorrere la distanza fra i due punti, uguagliamo prima le due forse e ricaviamo l'accelerazione della particella:
Poiché non conosciamo il valore del campo elettrico, ma abbiamo la differenza di potenziale e lo spostamento della particella, esprimiamo il campo elettrico in funzione di essi:
Ora, per ricavare il tempo utilizziamo la formula dello spazio nel moto uniformemente accelerato di una particella e ricaviamo la formula inversa:
Accedi a tutti gli appunti
Tutor AI: studia meglio e in meno tempo
