Concetti Chiave
- Due cariche elettriche puntiformi generano un campo elettrico in ogni punto dello spazio circostante.
- Esiste un punto specifico sulla retta tra le due cariche dove il campo elettrico risultante è nullo.
- L'esercizio richiede di trovare la distanza dalla seconda carica a questo punto di annullamento.
- Utilizzando la legge di Coulomb, si imposta un'equazione di secondo grado per determinare il punto di equilibrio.
- La soluzione dell'equazione indica che il punto di annullamento si trova a 0,86 m dalla seconda carica.
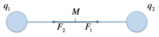
Quando due cariche elettriche puntiformi si trovano nello spazio, esse generano un campo elettrico in ogni punto dello spazio. Quindi, il campo elettrico ha un valore anche in ogni punto che si trova sulla retta congiungente le due cariche. Esiste un particolare punto, appartenente a questa congiungente, in cui i campi elettrici si annullano. Lo scopo dell'esercizio seguente sarà proprio quello di determinare tale punto.
Testo dell'esercizio
Due cariche puntiformi
e
si trovano nel vuoto a una distanza di
come in figura.
A quale distanza dalla seconda carica si trovano i punti, sulla retta che congiunge le due cariche, il cui il campo elettrico generato dalle stesse si annulla?
Svolgimento dell'esercizio
Chiamiamo
la distanza che separa il punto in cui il campo elettrico è nullo dalla seconda carica.
Poiché in quel punto il campo elettrico è nullo, sappiamo che in quel punto sono nulle anche le forze che agiscono.
Di conseguenza, possiamo affermare che nel punto
i vettori forza che dipendono dalle due cariche sono uguali e contrari, in particolare coincidono i moduli delle due forze:
.
Applicando ora la legge di Coulomb:
Osserviamo che si ricava un'equazione di secondo grado nella variabile
, poiché la distanza
è già nota.
Risolviamo ora l'equazione determinando
:
Ricordando che prodotto dei medi uguale prodotto degli estremi si ricava:
Sviluppiamo i conti togliendo le parentesi:
E infine:
Ovvero:
Sostituiamo i valori numerici adesso:
Si ottiene l'equazione di secondo grado:
da cui ricaviamo, utilizzando la formula risolutiva, che:
I punti richiesti si trovano quindi a
dalla seconda carica.
Domande da interrogazione
- Qual è l'obiettivo dell'esercizio descritto nel testo?
- Quali sono i valori delle cariche puntiformi e la loro distanza?
- Come si determina il punto in cui il campo elettrico è nullo?
- A quale distanza dalla seconda carica si trova il punto in cui il campo elettrico si annulla?
L'obiettivo dell'esercizio è determinare il punto sulla retta che congiunge due cariche puntiformi dove il campo elettrico generato dalle cariche si annulla.
Le cariche puntiformi hanno valori di [math] q_1 = 7 \cdot 10^{-2} C [/math] e [math] q_2 = 4 \cdot 10^{-2} C [/math], e si trovano a una distanza di [math] 2,00 m [/math] l'una dall'altra.
Si determina risolvendo un'equazione di secondo grado derivata dall'uguaglianza dei moduli delle forze elettriche generate dalle due cariche, applicando la legge di Coulomb.
Il punto in cui il campo elettrico si annulla si trova a [math]0,86 m[/math] dalla seconda carica.
Accedi a tutti gli appunti
Tutor AI: studia meglio e in meno tempo
