
L'esame di maturità del liceo scientifico si avvicina e, quindi, è bene iniziare ad esercitarsi per affrontare al meglio la prova di matematica 2015. Può essere utile, a tal proposito, svolgere le operazioni con calcolo degli indici statistici di base per variabili doppie. Il prof di matematica, Francesco Bologna, ci spiega come affrontare questo problema sia con il metodo tradizionale, sia con l'aiuto di una delle calcolatrici scientifiche più diffuse, la Casio FX991ES PLUS.
Scopri tutte le tracce della maturità scientifica degli anni passati
Impara ad usare la calcolatrice, guarda il nostro video!
CALCOLO DEGLI INDICI STATISTICI DI BASE PER VARIABILI DOPPIE
Le indicazioni nazionali riguardanti gli obiettivi specifici di apprendimento dell'allievo del liceo hanno previsto che, al termine del percorso liceale, lo studente dovrà conoscere i concetti salienti relativi al calcolo delle probabilità e dell'analisi statistica.
In particolare tra gli obiettivi specifici di apprendimento viene dato risalto al paragrafo "Dati e previsioni'' nel quale viene esplicitato che l'allievo dovrà saper distinguere tra caratteri qualitativi, quantitativi discreti e quantitativi continui, operare con distribuzioni di frequenze e rappresentarle.
Dovrà, inoltre, aver assimilato le definizioni e le proprietà dei valori medi e delle misure di variabilità, saper ricavare semplici inferenze, nonchè l'uso strumenti di calcolo (calcolatrice, foglio di calcolo) per analizzare raccolte di dati e serie statistiche.
Nel secondo biennio e nell'ultimo anno, in ambiti via via più complessi, l'allievo dovrà acquisire i concetti relativi alle distribuzioni doppie condizionate e marginali, alla deviazione standard, dipendenza, correlazione e regressione, e di campione.
Studierà la probabilità condizionata e composta, la formula di Bayes e le sue applicazioni, nonchè gli elementi di base del calcolo combinatorio, concludendo con lo studio di alcune distribuzioni discrete e continue di probabilità (come la distribuzione binomiale, la distribuzione normale, la
distribuzione di Poisson).
In questo paragrafo affrontiamo il calcolo degli indici statistici di base per variabili doppie.
CALCOLO DEGLI INDICI STATISTICI DI BASE PER VARIABILI DOPPIE
Esempio: Con riferimento ai dati della seguente tabella, si calcoli:
-
1. La media aritmetica dei dati della variabile
-
2. La deviazione standard della variabile
-
3. La retta di regressione.
| Anno | [math]x[/math] |
[math]y[/math] |
| 2001 | 3,45 | 5,56 |
| 2002 | 3,76 | 5,22 |
| 2003 | 3,55 | 6,23 |
| 2004 | 3,87 | 6,12 |
| 2005 | 3,68 | 6,45 |
1. La media aritmetica, media geometrica e la media quadratica
La media aritmetica è il tipo di media più comunemente usata. Essa viene calcolata sommando tutti i valori a disposizione e dividendo il risultato per il numero totale dei dati.
Come media aritmetica della variabile
si avrà:
Allo stesso modo per la variabile
si avrà:
2. Lo scostamento quadratico medio (deviazione standard)
La deviazione standard è uno dei modi per esprimere la dispersione dei dati intorno ad un indice di posizione, quale può essere, ad esempio, la media aritmetica.
Essa ha pertanto la stessa unità di misura dei valori e in statistica può esprimere la precisione dei dati.
Per determinare lo scostamento quadratico medio è necessario sviluppare la relazione:
Quindi si avrà:
=0,149[/math]
Procedendo allo stesso modo per la variabile
si avrà:
3. La retta di regressione.
L'obiettivo è quello di determinare la curva che, meglio di ogni altra, approssimi la serie di dati forniti.
Ovviamente le curve possibili possono essere di diverso tipo (una retta, una curva esponenziale, una funzione potenza, etc.). Nella consegna viene però esplicitato di cercare l'equazione di una retta.
Un metodo per definire quale sia la miglior funzione, largamente utilizzato, è il metodo dei minimi quadrati.
Tale metodo, nel caso della funzione lineare, è la retta di equazione
che minimizza la somma dei quadrati degli scarti, cioè per la quale è minima la quantità, che è funzione di
e
Per ottenere i valori dei coefficienti
e
della retta dovremo procedere nel seguente modo.
Risolviamo la seguente tabella:
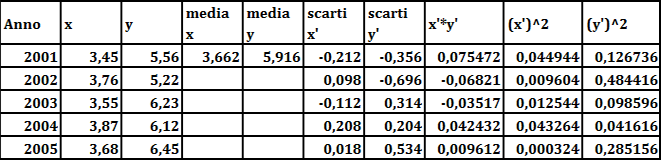
Ricordiamo che la retta ricercata sarà della forma:
(espres. N.1)
Con:
Quindi si avrà:
Sostituendo i valori determinati nella espressione N.1, si otterrà la retta cercata:
Vediamo come la calcolatrice FX991ES+ può rendere la procedura di calcolo molto semplice.
La FX991ES+ consente una efficace gestione e calcolo degli indici statistici di base per le variabili doppie. Impostiamo la calcolatrice nel modo opportuno.
Passaggio #1
Attraverso al combinazione:
Collochiamoci nel menù STAT.
Successivamente selezioniamo la voce
Relative alle variabili singole.
Passaggio #2
Digitiamo i valori della variabile nel foglio di calcolo e usciamo con il tasto AC.
-scheda4.png)
Passaggio #3
Tramite la combinazione:
Ci collocheremo nel menù di calcolo.
-scheda4.png)
Passaggio #4
Digitiamo 4 per effettuare i calcoli richiesti.
In questo menù 1: n restituisce il numero di righe, 2: e 5: le medie aritmetiche delle variabili, 3: e 5: le deviazione standard della popolazioni; 4: e 6: le deviazioni standard dei campioni.
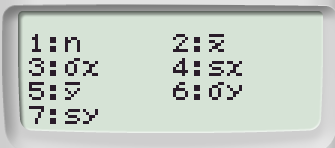
Passaggio #5
Possiamo quindi procedere al calcolo della media aritmetica digitando 2 seguito dall'uguale (=).
Successivamente, attraverso al combinazione
Potremo ottenere con l'opzione 3 la deviazione standard.

Passaggio #6
Procediamo allo stesso modo per la variabile
.
Possiamo quindi procedere al calcolo della media aritmetica digitando:
Scegliamo l'opzione 5 seguito dall'uguale (=).
Successivamente, attraverso al combinazione:
Potremo ottenere con l'opzione 6 la deviazione standard.

Passaggio #7
Per determinare i coefficienti della retta di regressione, digitiamo:
Successivamente 1: per ottenere il coefficiente A e 2: per il coefficiente B
Oss. Ricorda che il modello di regressione della calcolatrice è
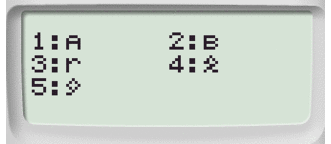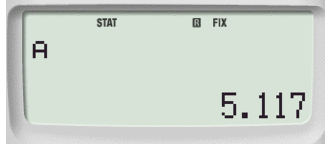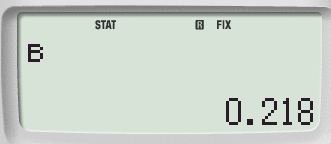






 Accedi a tutti gli appunti
Accedi a tutti gli appunti
 Tutor AI: studia meglio e in meno tempo
Tutor AI: studia meglio e in meno tempo