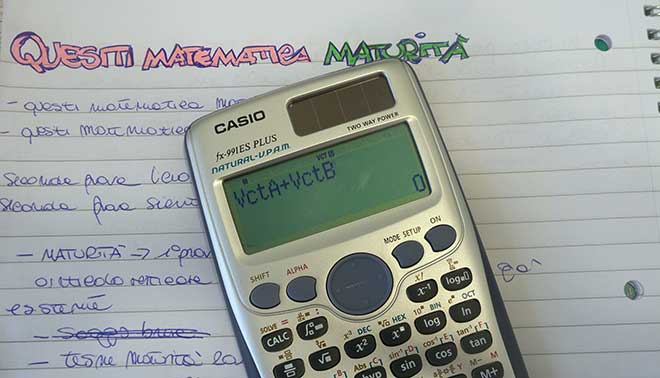
L'esame di maturità del liceo scientifico si avvicina e, quindi, è bene iniziare a prepararsi per affrontare al meglio la prova di matematica 2015. Può essere utile, a tal proposito, svolgere le operazioni con analisi del calcolo vettoriale. Il prof di matematica, Francesco Bologna, ci spiega come affrontare questo problema sia con il metodo tradizionale, sia con l'aiuto di una delle calcolatrici scientifiche più diffuse, la Casio FX991ES PLUS.
Scopri tutte le tracce della maturità scientifica degli anni passati
Impara ad usare la calcolatrice, guarda il nostro video!
CALCOLO VETTORIALE
Le indicazioni nazionali riguardanti gli obiettivi specifici di apprendimento dell'allievo del liceo hanno previsto che, al termine del percorso liceale, lo studente dovrà conoscere i concetti salienti relativi al calcolo matriciale.
Nel paragrafo "Aritmetica e algebra" viene esplicitato che saranno ripresi e approfonditi i concetti di vettore, di dipendenza e indipendenza lineare, di prodotto scalare e vettoriale nel piano e nello spazio. E' lasciata alla scelta dell'insegnante l'introduzione del calcolo matriciale.
In questo paragrafo affrontiamo l'analisi del calcolo vettoriale.
CALCOLO VETTORIALE
In matematica un vettore è un elemento di uno spazio vettoriale.[1] I vettori sono quindi oggetti che possono essere sommati fra loro e moltiplicati per dei numeri, detti scalari.
I vettori sono comunemente usati per indicare grandezze che sono completamente definite solo quando sono specificati sia modulo che una direzione ed un verso rispetto ad un altro vettore.
I vettori sono definiti come facenti parte di uno spazio vettoriale; il piano cartesiano essendo un esempio di spazio vettoriale consente di rappresentare un vettore un punto del piano cartesiano determinato da una coppia di numeri reali
Disegnando una freccia che parte nell'origine
e arriva in
si ottiene la rappresentazione geometrica del vettore
Nello spazio tridimensionale un vettore E' analogamente una terna di numeri reali
Esercizi:
Dati i vettori:
Calcola:
1. la somma
2. il modulo del vettore
3. il prodotto scalare
4. il modulo del prodotto vettoriale
Esercizio 1.
La somma e la differenza tra i vettori si ottiene semplicemente addizionando o sottraendo reciprocamente le coordinate dei vettori.
Si avrà:
Esercizio 2.
Il modulo del vettore a si otterrà attraverso la relazione:
Esercizio 3.
Il prodotto scalare tra due vettori e un prodotto che pur moltiplicando due vettori restituisce per risultato un numero.
Si otterrà attraverso la relazione:
Esercizio 4.
Dati due vettori
e
, chiamiamo prodotto vettoriale di
e
il vettore
che ha per modulo il valore:
Vediamo come la calcolatrice FX991ES+ può rendere la procedura di calcolo molto semplice.
Passaggio #1
Attraverso al combinazione:
Collochiamoci nel menù VECTOR
-scheda10.png)
Passaggio #2
Digitiamo 1: e selezioniamo il vettore A: VctA
Selezioniamo l'ordine 2.
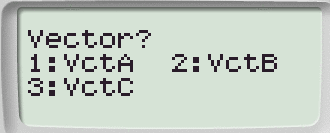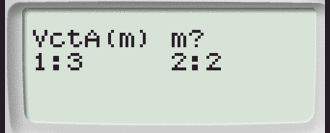
Passaggio #3
Tramite il tasto cursore inseriamo i valori:
-scheda10.png)
Usciamo con il tasto AC.
-scheda4.png)
-scheda10.png)
Passaggio #4
Digitiamo
E digitiamo il tasto 2.
Potremo in tal modo, selezionando il vettore B, ripetere la procedura e memorizzare i dati.
Usciamo con il tasto AC.
-scheda4.png)
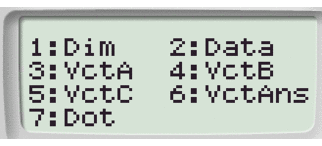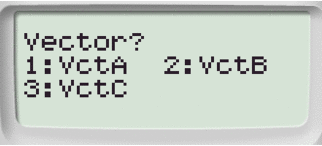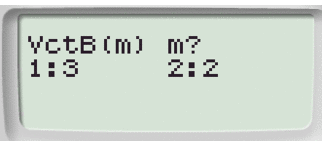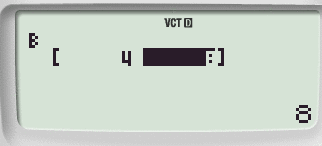
Passaggio #5
Collochiamoci nel menù di calcolo tramite la combinazione:
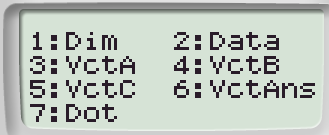
Passaggio #6
Per effettuare le varie operazioni inseriamo i due vettori digitando successivamente:
-scheda10.png)
Passaggio #7
Tramite il tasto cursore inseriamo l'operazione richiesta
-scheda10.png)
Seguito da
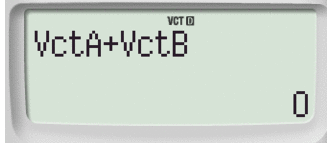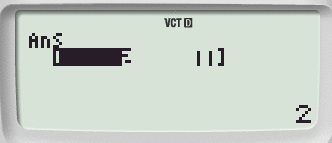
Passaggio #8
Digitando
Ritorneremo alla schermata precedente.
Così facendo potremo inserire sia l'operazione di prodotto scalare (DOT) che quello vettoriale x.
Ricorda che per inserire l'operazione di prodotto scalare (DOT)
E' necessario seguire la combinazione:
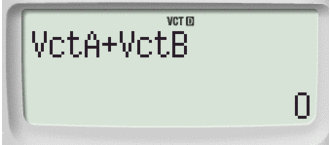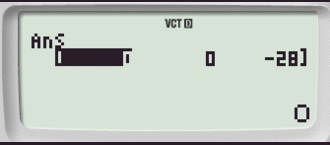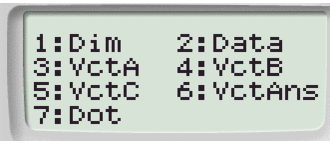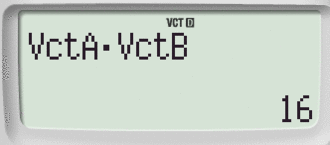
Passaggio #9
Per il calcolo del modulo basterà anteporre a VctA il comando Abs attraverso la sequenza:
-scheda10.png)
-scheda10.png)






 Accedi a tutti gli appunti
Accedi a tutti gli appunti
 Tutor AI: studia meglio e in meno tempo
Tutor AI: studia meglio e in meno tempo