Risolvere il seguente triangolo rettangolo
[math](alpha=90^circ)[/math]
[math]b=12\sqrt3; gamma=30^circ[/math]
In questo caso ci è noto la misura del cateto e dell'angolo acuto
[math]gamma[/math]
, oltre all'angolo retto
[math]alpha=90^circ[/math]
.
Quindi poichè la somma degli angoli interni di un triangolo è di
[math]180^circ[/math]
, ovvero
[math]alpha+eta+gamma=180^circ[/math]
si ha che
[math]90^circ+30^circ+eta=180^circ => eta=180^circ-90^circ-30^circ=60^circ[/math]
.
Pertanto
[math]eta=60^circ[/math]
.
In un triangolo rettangolo un cateto è uguale al prodotto dell'ipotenusa
per il seno dell'angolo opposto al cateto stesso
[math]b=a\\sin (eta) => a=b/(\\sin(eta))=(12\sqrt3)/{\\sin(60^circ)}=(12\sqrt3)/((\sqrt3)/2)=24[/math]
;
inoltre in un triangolo rettagolo un cateto è uguale al prodotto
dell'altro cateto per la cotangente dell'angolo acuto ad esso adiacente
[math]c=bcotg(eta)=12\sqrt3cotg{60^circ}=12\sqrt3 \cdot (\sqrt3)/3=12[/math]
.
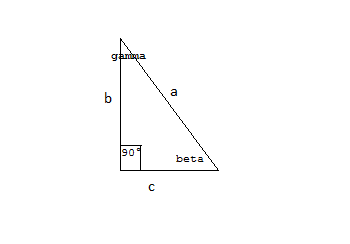
Accedi a tutti gli appunti
Tutor AI: studia meglio e in meno tempo
