Discontinuità - Definizione e tipi di discontinuità

In questo appunto viene approfondito il concetto di discontinuità di una funzione, viene fornita una definizione di discontinuità, degli esempi e i diversi tipi di discontinuità.

Discontinuità

Una funzione si dice discontinua se esiste almeno un punto in cui il limite della funzione non è definito.

Un limite non è definito quando il limite destro e il limite sinistro non coincidono (non hanno lo stesso valore), sottoforma di espressione matematica si può dire che:

Dove x è la variabile indipendente della funzione, y è la variabile dipendente della funzione mentre

è un valore definito della variabile x.

Un altro esempio in cui la funzione non è continua si ha quando il limite per x che tende a

finito) assume un valore infinito.

Riportiamo in seguito diversi casi in modo da comprendere meglio quando la funzione può essere definita continua o discontinua.

• Se
  [math]\lim_{x \to x_o^+} f(x)=2[/math]
  [math]\lim_{x \to x_o^-} f(x)=5[/math]

  Si ha che il limite destro e il limite sinistro in un punto (

  [math]x_0[/math]
  ) assumono valori differenti perciò la funzione ha un punto di discontinuità in
  [math]x_0[/math]
• Se
  [math]\lim_{x \to x_o^+} f(x)=\infty[/math]

  Oppure se

  [math]\lim_{x \to x_o^-} f(x)=\infty[/math]

  Si ha che il limite destro o sinistro della funzione in un punto (

  [math]x_0[/math]
  ), quindi in un punto che ha valore definito, assume valore infinito perciò la funzione in quel punto non è continua.
• Se
  [math]\lim_{x \to \infty} f(x)=\infty[/math]

  Oppure se

  [math]\lim_{x \to \infty} f(x)=\infty[/math]

  Il limite della per x che tende a

  [math]\pm\infty[/math]
  non determina se la funzione è continua o discontinua perciò se tale limite ha valore infinito non significa che la funzione è continua o discontinua, per verificare la continuità o la discontinuità è necessario controllare i limiti della funzione negli altri punti.

Tipi di discontinuità

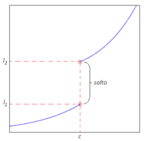
• Discontinuità di prima specie: s
  i dice che in x=c la funzione f(x) ha un punto di discontinuità di prima specie quando esistono finiti il limite destro e sinistro, ma sono diversi tra loro (La differenza in valore assoluto tra i due si chiama salto).
  Se si rappresenta la funzione in un piano cartesiano (piano in cui vengono rappresentate negli assi le coordinate x e y) si nota come la funzione esiste per tutti i valori della x però esiste un punto in cui la funzione assume valori diversi se ci si avvicina da destra o da sinistra, in entrambi i casi la funzione assume dei valori finiti.
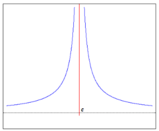
• Discontinuità di seconda specie:
  si dice che in x=c la funzione f(x) ha un punto di discontinuità di seconda specie quando almeno uno dei due limiti non esiste, o non esiste finito.
  In questo caso si può avere ad esempio che il grafico della funzione tende ad infinito se ci si avvicina a
  [math]x_0[/math]
  da una parte mentre tende ad un valore definito se ci si avvicina dalla parte opposta.
  
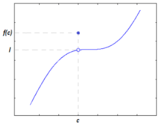
• Discontinuità di terza specie: si dice che in x=c la funzione f(x) ha un punto di discontinuità di terza specie (eliminabile) quando esiste finito il limite per x-->c di f(x) ma f(c) non esiste o è diverso da f(x).
  In questo caso se si rappresenta la funzione in un piano cartesiano si noterà come la funzione presenti un buco, ovvero esiste un punto in cui la funzione non esiste anche se i limiti destro e sinistro in quel punto esistono e coincidono.
  Sottoforma di espressione matematica si può scrivere che:
  
  [math]\lim_{x \to x_o^+} f(x) = \lim_{x \to x_o^-} f(x)[/math]
  [math]f(x_0) =[/math]
  non esiste

Discontinuità di una funzione composta

In genere è necessario dimostrare che una funzione, anche complessa, sia continua o discontinua, per fare ciò si potrebbe verificare che in ogni punto la funzione sia continua perciò sarebbe necessario verificare che il limite destro e il limite sinistro coincidono.
Tale procedimento dovrebbe essere fatto in ogni punto del grafico e si può immaginare che un tale procedimento richieda un grande dispendio di tempo.

In genere, infatti, per dimostrare se una funzione è continua o discontinua si utilizza il seguente postulato:
Una funzione composta è continua se sono continue anche le funzioni che la compongono.

Perciò è sufficiente verificare che le funzioni che la compongono sono continue.
Riportiamo in seguito le funzioni elementari che sono continue:

• funzione costante:
  [math]y=costante[/math]
  (in un piano cartesiano tale funzione è rappresentata da una retta orizzontale)
• funzione polinomiale:
  [math]y=x[/math]
  ,
  [math]y=x^2[/math]
  (funzione che contiene un polinomio di qualsiasi grado, possono anche essere presenti dei termini noti)
• funzione esponenziale:
  [math]y=e^x[/math]
• funzione logaritmica:
  [math]y=ln(x)[/math]
  (tutte le funzioni logaritmiche sono continue nel suo dominio, indipendentemente dalla base del logaritmo)

Un esempio di una funzione non continua è:

Tale funzione non è definita in x=0 e in tale punto i limiti della funzione tendono ad infinito.
È possibile tuttavia ridurre il dominio ai numeri positivi o solamente negativi e in tal modo si ottiene una funzione continua in tale intervallo.
Per ulteriori approfondimenti sulle funzioni continue vedi anche qua