Concetti Chiave
- L'animazione genera un effetto caleidoscopico utilizzando curve polari in movimento.
- Quattro curve polari per ogni varietà di rosa sono usate per creare il grafico di base.
- Le curve si espandono e contraggono mentre ruotano con diverse velocità durante l'animazione.
- La pressione del tasto F5 ricarica la pagina per riprendere il movimento delle immagini.
- Le funzioni matematiche definiscono le dilatazioni e contrazioni dei petali e le forme delle rose.
Descrizione
Un numero di curve in forma polare disegnate e configurate per l'animazione producono un effetto caleidoscopico. Il grafico di base consiste di quattro curve polari per ogni varietà di rosa. Tutte e quattro le curve vengono ruotate (con diverse velocità) sopra l' animazione mentre si espandono e si contraggono.
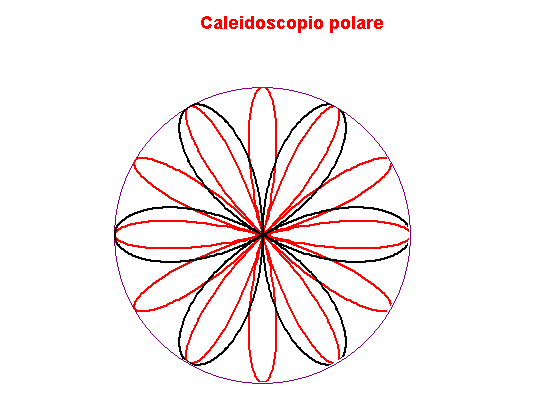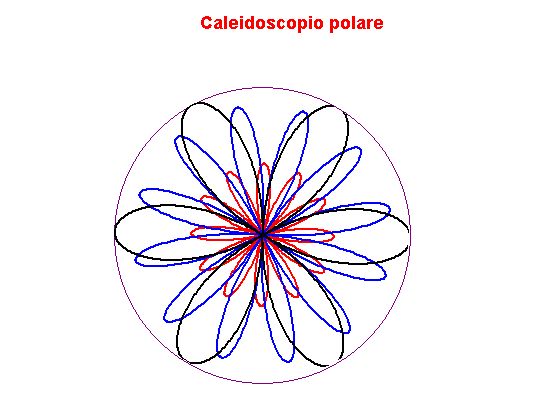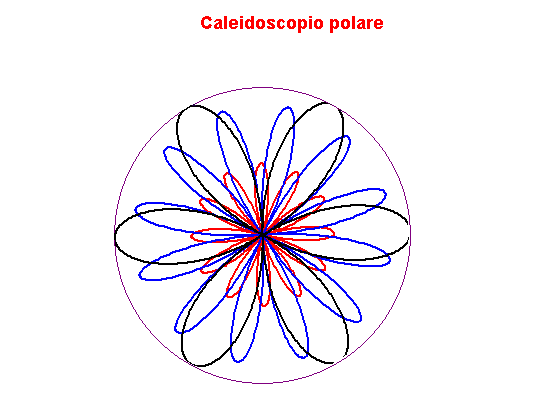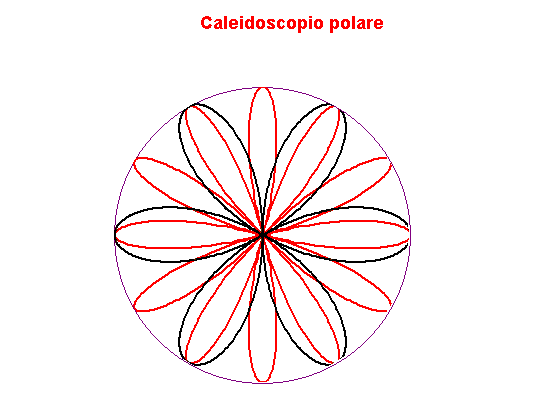
Se l'immagine ha messo di ruotare premi il tasto F5 per ricaricare la pagina e far ricominciare il movimento.
Parametri Interessati
[math]p_1=6[/math]
dilatazione e contrazione dei petali
[math]p_2=6[/math]
[math]p_3=3[/math]
Calcoli associati
[math]A_1=\\cos(k/100 \cdot 2\pi)[/math]
espressioni che definiscono i raggi per le dilatazioni e le contrazioni dei petali
[math]A_2=\\sin (k/100 \cdot 2\pi)[/math]
[math]r_1( heta)=A_1 \cdot \\cos(p_1 heta)[/math]
funzioni che definiscono le quattro rose
[math]r_2( heta)=A_2 \cdot \\cos(p_2 heta+\pi/2)[/math]
[math]r_3( heta)=\\cos(p_3 heta)[/math]
[math]r_4( heta)=r^3( heta+\pi)[/math]
Accedi a tutti gli appunti
Tutor AI: studia meglio e in meno tempo
