 PROBLEMA 1 - PNI - 2013
PROBLEMA 1 - PNI - 2013Punto 1
f:\left[0, +\infty\right) \rightarrow \mathbb{R}, f \in C^2 \left( \left[0, +\infty\right) \right)\\
y=2x \text{ tangente a } \Gamma \text{ in } \left(2,4\right)\\
\text{Poiché } f''\left(2\right)=0 \text{ e inoltre si ha }\\
f''\left(x\right) > 0 \text{ per } x \in \left(2-\epsilon, 2 \right)\\
f''\left(x\right) \text{con } \epsilon > 0, \text{ ne segue che } x_0=2 \text{ punto di massimo per } f'\left(x \right).\\
\text{Inoltre essendo } f'\left(2\right)=2 \text{ (coefficiente angolare della retta tangente)}\\ \text{si ha che il massimo di } f' \text{ ha coordinate } A\left(2,2\right).\\
\text{Poiché } f'' \leq f' \leq f \; \forall x \in \left[0, +\infty \right) \text{ e si ha }\\
lim_{x\to +\infty}f\left(x\right)=0 \Rightarrow lim_{x\to +\infty}\frac{f\left(x\right)}{x}=0\\
\text{e per Hopital }lim_{x\to +\infty} f'\left(x\right)=0 \text{ e quindi } y=0 \text{ asintoto orizzontale di } f'\\
\text{Inoltre poiché}\\
f' \text{ cresce su } \left[0, 2\right)\\
f' \text{decresce su } \left(2, +\infty \right)
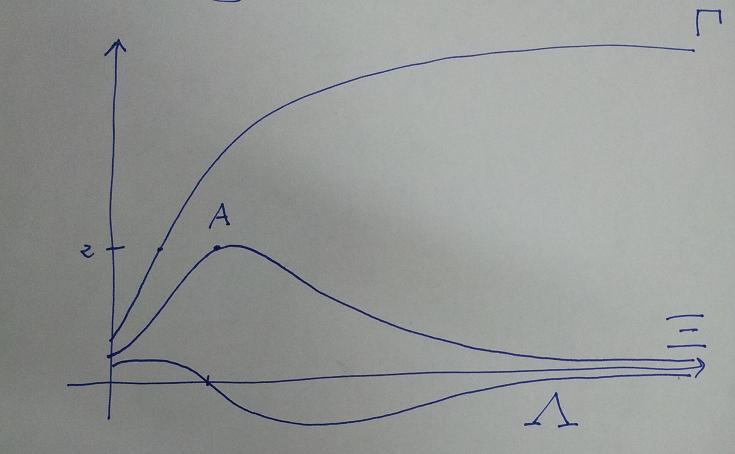
\text{il grafico } \Xi, \text{ probabile, è il seguente:}
[/math]
--------------------------------------------------
Punto 2
La presenza dell'asintoto orizzontale indica che, dopo un certo intervallo di tempo, la popolazione tende ad assestarsi attorno ad un valore costante. Essendo
strettamente crescente, la popolazione è in crescita, tuttavia la presenza del flesso implica che, su
tale crescita sia accelerata
mentre risulta decelerata per
--------------------------------------------------
Punto 3
\text{Poiché }lim_{x \to +\infty}f\left( x \right)=8 \text{ si ha }\\
8=a \cdot lim_{x \to +\infty} \frac{1}{1+e^{b-x}}=a \cdot 1\\
\Rightarrow a=8\\
\text{Inoltre, essendo } f'\left(2\right)=2 \text{ si ha }\\
f'\left( x \right) = -a \cdot \left( 1 + e^{b-x}\right)^-2 \cdot \left(-e^{b-2}\right)\\
\Rightarrow 2=-8\left(1+e^{b-2}\right)^{-2} \cdot \left(-e^{b-2}\right)\\
\text{posto } t=e^{b-2} \text{ si ha }\\
1=\frac{4e^t}{\left(1+e^t\right)^2} \Rightarrow 1+e^{2t}+2e^t=4e^t\\
e^{2t}-2e^{t}+1=0\\
\left(e^t-1 \right)^2=0\\
e^t=1 \Rightarrow f=0 \Rightarrow b-2=0 \Rightarrow b=2
[/math]
--------------------------------------------------
Punto 4
A=\int_0^2 f'' \left( t \right) dt = \left[ f'\left( t \right) \right]_0^2=f'\left(2\right)-f'\left(0\right)=\\
2-\frac{8e^2}{\left( 1+e^2 \right)^2} \text{ essendo } f'\left(x\right)=\frac{8e^{2-x}}{\left( 1+ e^{2-x}\right)^2}
[/math]



 Accedi a tutti gli appunti
Accedi a tutti gli appunti
 Tutor AI: studia meglio e in meno tempo
Tutor AI: studia meglio e in meno tempo