Jacko
di Giacomo Del Lungo
Immagine autore
9' di lettura 9' di lettura
Matematica PNI - Soluzione quesiti articolo

Matematica PNI - Soluzione quesito 1

Si ha un triangolo di lati a=2; b=3 e area A=3. Si vuole determinare il terzo lato c.

Utilizzando la formula di Erone per il calcolo delle aree di un triangolo si ha:

[math]A=\sqrt{p(p-a)(p-b)(p-c)}[/math]

dove p è il semiperimetro del triangolo.

Da qui, moltiplicando e risolvendo rispetto alla c si trova l'equazione biquadratica:

[math]c^{4}-26c^{2}+169=0[/math]

Da qui si ottengono le due soluzioni reali

[math]\sqrt{13}[/math]
[math]-\sqrt{13}[/math]

di cui l'unica ammissibile è

[math]c=\sqrt{13}[/math]

Aggiungici su WhatsApp per ricevere aggiornamenti a portata di tap! Aggiungici su WhatsApp per ricevere aggiornamenti a portata di tap!

Matematica PNI - Soluzione quesito 2

Si ha che la derivata della funzione

[math]F[x]=f(x)-f(2x)[/math]
in x=1 vale 5 e in x=2 vale 7.

Si vuole trovare la derivata della funzione

[math]G[x]=f(x)-f(4x)[/math]
in x=1.

Poichè

[math]F^{'}[x]=f^{'}(x)-2f^{'}(2x)[/math]
e si ha pure
[math]G'(x)=f'(x)-4f'(4x)[/math]
otteniamo

[math]f'(1)-2f'(2)=5\\ f'(2)-2f'(4)=7[/math]

da cui, moltiplicando la seconda per due e sommando membro a membro

[math]f'(1)-2f'(2)+2f'(2)-4f'(4)=5+14[/math]

e quindi

[math]G'(1)=f'(1)-4f'(4)=19[/math]

Matematica PNI - Soluzione quesito 3

Si cerca l'equazione della retta passante per il punto B(-6;-8 ) che abbia distanza massima dal punto A(2;-1).

Chiamata

[math]r: y = mx+q[/math]
la retta cercata, abbiamo, per l'appartenenza del punto B, che

[math]-8 = -6m +q[/math]
(1)

Ora dobbiamo imporre la massima distanza dal punto A di r.

La distanza è data da
[math]d=\frac{y_{0}-mx_{0}-q}{\sqrt{1+m^{2}}}[/math]
dove
[math]y_{0}[/math]
e
[math]x_{0}[/math]
sono le coordinate del punto A.

Dunque basta cercare i punti di massimo della funzione

[math]d=\frac{-1-2m-q}{\sqrt{1+m^{2}}}=\frac{7-8m}{\sqrt{1+m^{2}}}[/math]
ottenuta tenendo conto della condizione (1)

studiandone il segno della derivata

[math]d^{'}=\frac{-8\sqrt{1+m^{2}}-\frac{(7-8m)2m}{2\sqrt{1+m^{2}}}}{1+m^{2}}[/math]

Così facendo si ottiene

[math]m=-\frac{8}{7}; q=-\frac{104}{7}[/math]

Matematica PNI - Soluzione quesito 4

Di un tronco di piramide retta si sonoscono l'altezza h e i lati delle basi a e b.Si Cerca il volume V.

Si ha per il volume di un tronco di piramide retto che il volume è uguale a

[math]V=\frac{h}{3}(A+a+\sqrt{A*a})[/math]

dove A e a sono le aree delle due basi, quindi nel nostro caso una sarà

[math]a^{2}[/math]
e una
[math]b^{2}[/math]

Matematica PNI - Soluzione quesito 5

Se per la dilatazione corrispondente a un certo aumento della temperatura un corpo si allunga di una certa percentuale
in tutte le le direzioni la sua superficie si accresce di proporzione doppia, per la legge di dilatazione lineare

[math]l = l_{0}(1+\lambda t)[/math]

dove lambda è il coefficiente di dilatazione lineare, t è la temperatura finale del corpo (se supponiamo che parta da
zero gradi centigradi (altrimenti rappresenta la differenza di temperatura), l la lunghezza finale ed

[math]l_{0}[/math]
quella iniziale.

Invece il suo volume accrescerà in proporzione tripla per la legge di dilatazione termica cubica:

[math]V=a_{0}(1+\lambda t)b_{o}(1+\lambda t)c_{o}(1+\lambda t)=V_{0}(1+3\lambda t)[/math]

dove

[math]a_{0};b_{0};c_{0}[/math]
sono le dimensioni iniziali del corpo, e dove abbiamo trascurato
[math]\lambda ^{2}[/math]
e
[math]\lambda ^{3}[/math]
.

Matematica PNI - Soluzione quesito 6

Il numero più piccolo che possiamo ottenere è 1234567.

Per ottenere il numero che occupa la settima posizione basta tener presente che le permutazionipossibili
delle ultime tre cifre (5, 6 e 7) sono 6. Quindi il numero immediatamente più grande si otterrà scambiando il posto
del 4 e del 5 ed è:

1235467.

Per quanto riguarda la 721 posizione teniamo presente che 6! = 720, e sarebbero tutte le permutazioni delle ultime
sei cifre partendo sempre dal numero più piccolo possibile 1234567.

Quindi il numero che occupa la 721a posizione sarà quello ottenuto invertendo l'1 ed il 2 e cioè:

2134567.

Matematica PNI - Soluzione quesito 7

In un gruppo di 10 persone il 60% ha gli occhi azzurri. Dal gruppo si selezionano a casa due persone. Quale è la
probabilità che nessuna di essere abbia occhi azzurri?

La risposta è 13%.
Infatti la probabilità che la prima persona considerata non abbia gli occhi azzurri è:

[math] \frac{4}{10} [/math]

essendo 4 le persone non dotate di occhi azzurri e 10 le persone totali.

La probabilità che la seconda persona considerata non abbia gli occhi azzurri è:

[math] \frac{3}{9} [/math]

Basta moltiplicare queste due probabilità ed otteniamo:

[math] \frac{4}{30} [/math]

che corrisponde a 0,133333.

Matematica PNI - Soluzione quesito 8

Si mostri senza usare il Teorema di L'Hopital, che:

[math] lim_{x \to \pi} \frac{\exp senx -\exp sen\pi }{x-\pi} = -1
[/math]

Sappiamo dalla definizione di derivata che:

[math] f{(x_0)}' = \lim_{h \to 0} \frac{f(x_0 + h) -f(x_0) }{h}

[/math]

Quindi noi abbiamo la derivata della funzione

[math] e^{senx} [/math]

nel punto

[math] x=\pi [/math]

Quindi basta calcolare

[math] f^{'} {(\pi )} = e^{sen\pi }*cos\pi = -1 [/math]

Matematica PNI - Soluzione quesito 9

Gli irrazionali sono di più dei razionali.
La risposta deriva dal fatto che i numeri reali si possono vedere come unione di razionali e irrazionali. Poichè sappiamo da
Cantor che Q ed N sono equipotenti, mentre la potenza di R (la potenza del continuo) è superiore a quella di N, si ha come
logica conseguenza che i numeri irrazionali devono essre di più dei razionali perchè valga:

[math]R = Q\bigcup I[/math]
.

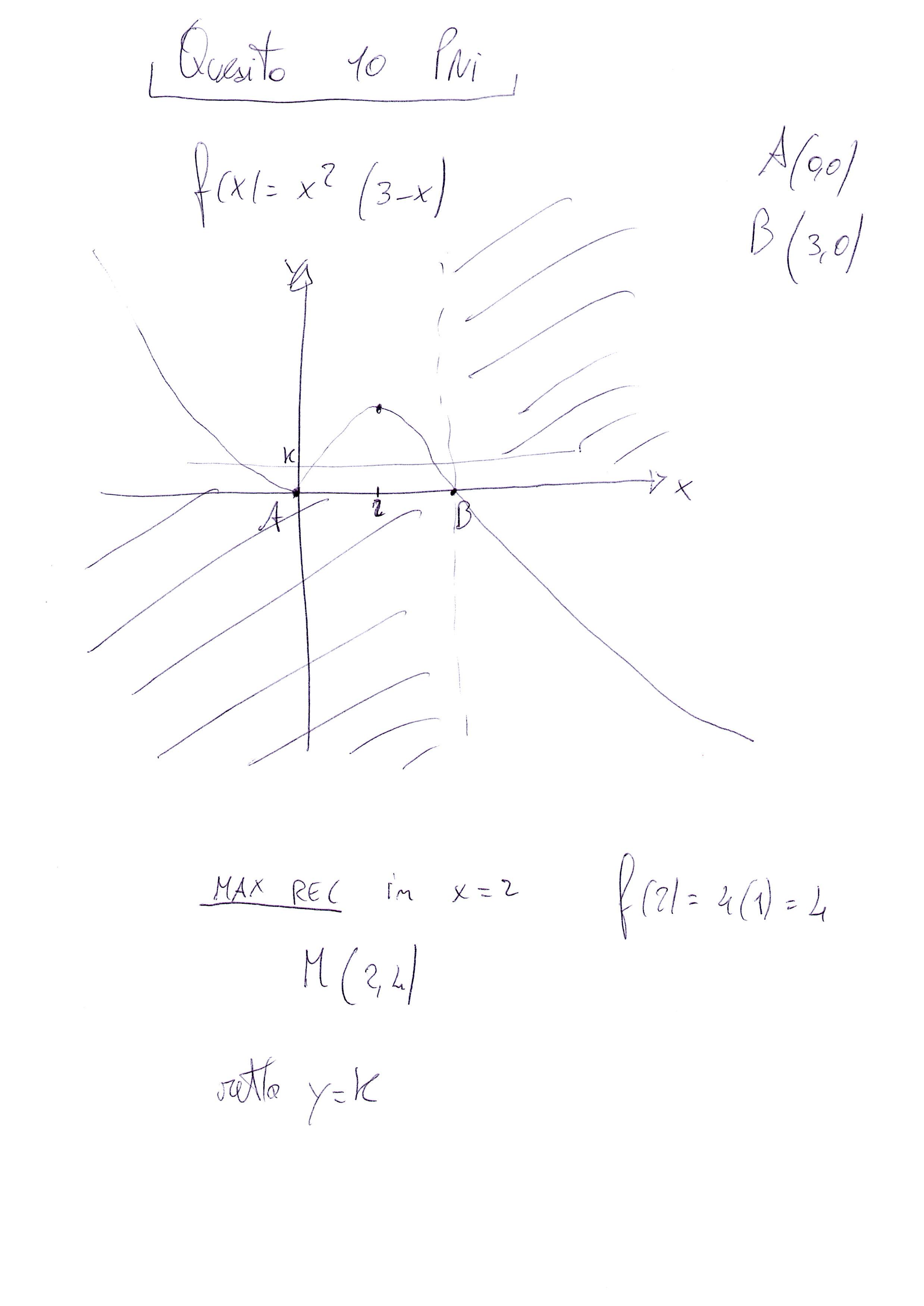
Matematica PNI - Soluzione quesito 10

Quesito 10

Per stabilire per quali valori di K la funzione ammette due soluzioni reali e distinte nell'intervallo [0,3]
ci rappresentiamo la funzione

[/math] f(x)=x^{2}(3-x) [/math]

(A meno di eventuali flessi il grafico è questo, non ci interessano).

Dal grafico notiamo che una la retta y=K avrà due intersezioni distinte con la curva (appartenenti all'intervallo [0,3])
per valori di k che vanno da 0 all'ordinata del massimo relativo (presente tra 0 e 3).
Studiando la derivata prima della funzione troviamo il punto di massimo relativo x=2. Il massimo sarà M(2,4).

Quindi per k appartenente all'intervallo [0,4).

Posto k = 3 usiamo il metodo di bisezione per approssimare la maggiore delle radici della funzione:

[math] f(x)=x^{2}(3-x)-3 [/math]

consideriamo che f(x) = 0 ha sicuramente la radice maggiore con x>2 (punto di massimo relativo della funzione).

Poniamo a0 = 2 e b0 = 3. Vediamo che f(2) = 1, ed f(3) = -3. Quando sono di segno opposto

consideriamo

[math] a_{n+1} = \frac{a_{n}+b_{n}}{2} [/math]
e

[math] b_{n+1} = b^{n} [/math]
. (In caso contrario lascio inalterato a e modifico b).

Quindi la soluzione cercata sarà sempre tra bn e an.

an

Quando an e bn cono uguali fino alla seconda cifra decimale possiamo fermarci.

Partendo da a0 = 2 e b0 = 3;
fino ad a4 = 11/4 e b4 = 45/16 troviamo 2,75