Soluzione 1 punto problema 1 indirizzo ordinario.
[math]f : [0 , 9] \to \mathbb{R}[/math]
[math] f(x) = \int_{0}^{x} [ \cos (\frac{1}{2}) + \frac{1}{2}] dt [/math]
Si ha:
[math] f'(x) = \cos (\frac{x}{2}) + \frac{1}{2}[/math]
Per cui:
[math] f'(x) = \cos (\frac{\pi}{2}) + \frac{1}{2} = \frac{1}{2}[/math]
[math] f'(x) = \cos (\frac{2\pi}{2}) + \frac{1}{2} = -\frac{1}{2}[/math]
Soluzione 2 punto problema 1 indirizzo ordinario.
[math]f'(x) = \cos (\frac{x}{2}) + \frac{1}{2}[/math]
f'(x) è periodica di periodo
[math]4\pi[/math]
. Il suo grafico coincide con quello della funzione [math]\cos t[/math]
ma dilatato sull'intervallo [math][0 , 4\pi][/math]
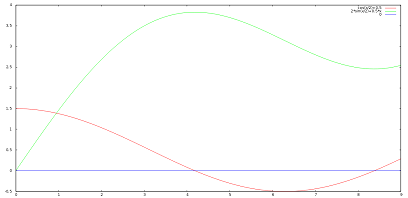
e traslato in alto di \frac{1}{2}. Il grafico è il seguente (in rosso):
Osserviamo che:
f'(x) = 0
[math]\cos \frac{x}{2} \pm - \frac{1}{2}[/math]
[math]\frac{x}{2} = \frac{2\pi}{3} \rightarrow x = \frac{4\pi}{3}[/math]
[math]\frac{x}{2} = \frac{4\pi}{3} \rightarrow x = \frac{8\pi}{3}[/math]
E in un intorno di tali punti la funzione f' cambia segno pertanto:
[math]X_o = \frac{4\pi}{3}[/math]
è un max di f
[math]X_o = \frac{8\pi}{3}[/math]
è un min di f
Inoltre f(0) = 0 per cui il probabile andamento di f è (la parte in verde del grafico precedente).
OSS: il minimo risulta positivo in quanto l'integrale tra 0 e
[math]\frac{8\pi}{3}[/math]
è la somma di due aree algebriche di cui la positiva (tra 0 e [math]\frac{4\pi}{3}[/math]
è maggiore negativa (tra [math]\frac{4\pi}{3} e \frac{8\pi}{3})[/math]
Soluzione 3 problema 1 indirizzo ordinario.
[math]M = \frac{1}{2\pi} \int_{0}^{2\pi} f'(t) dt = [/math]
[math]\frac{1}{2\pi} [f(t)]_{0}^{2\pi} =[/math]
[math]\frac{1}{2\pi} [\int_{0}^{2\pi} (\cos(\frac{x}{2}) + \frac{1}{2}) dx] [/math]
[math]\frac{1}{2\pi} [2 \sin (\frac{x}{2}) + \frac{x}{2}]_{0}^{2\pi} =[/math]
[math]\frac{1}{2\pi} [\pi] = \frac{1}{2}[/math]
Soluzione 4 punto problema 1 indirizzo ordinario.
[math]W = \int_{0}^{4} \; A(x) dx =[/math]
[math]\int_{0}^{4} [3 \sin (\frac{4x}{4})] dx =[/math]
[math][- \frac{12}{\pi} \cos (\frac{\pi x}{4})]_{0}^{4} =[/math]
[math]- \frac{12}{\pi} \cdot \cos(\pi) + \frac{12}{\pi} \cos(0) =[/math]
[math]\frac{12}{\pi} + \frac{12}{\pi} = \frac{24}{\pi}[/math]
Accedi a tutti gli appunti
Tutor AI: studia meglio e in meno tempo
