PROBLEMA 2 - PNI
Punto 1
[math]f\left(x\right) =x^3 \ln \left(x\right)[/math]
[math]\text{Dom}f=\left( 0, +\infty\right)[/math]
[math]f\left(x\right) > 0\Leftrightarrow \ln\left(x\right)>0 \Leftrightarrow x>1[/math]
[math]\lim_{x \to 0^+} f\left(x\right)=0[/math]
[math]\lim_{x \to +\infty} f\left(x\right)=+\infty \text{ nessun asintoto }[/math]
[math]f'\left(x\right)=3x^2 \ln \left(x \right) + x^3 \frac{1}{x}=[/math]
[math]3x^2 \ln \left(x\right) + x^2=x^2 \left(3 \ln \left(x\right)+x \right)\geq0 \Leftrightarrow 3\ln \left( x \right) +1 \geq0[/math]
[math]\ln \left( x \right) \geq -\frac{1}{3} \Rightarrow x \geq e^{-\frac{1}{3}}[/math]
[math]A \left( e^{-\frac{1}{3}, -\frac{1}{3e}}\right) \text{ minimo assoluto }[/math]
[math]- f \text{ cresce su }\left(e^{-\frac{1}{3}}, +\infty \right)[/math]
[math]- f \text{ decresce su } \left(0, e^{-\frac{1}{3}} \right)[/math]
[math]f''\left(x\right)=2x\left(3\ln\left(x\right) + 1 \right)+ x^2 \frac{3}{x}=[/math]
[math]6x\ln \left( x \right) + 2x+3x=x\left(6 \ln \left( x \right)+5\right)\geq 0[/math]
[math]6 \ln \left( x \right)+5 \geq 0[/math]
[math]x\geq e^{-\frac{5}{6}}[/math]
I valori approssimati sono:
[math]
-\frac{1}{3e}\simeq-0.123\\
e^{-\frac{1}{3}}\simeq0.717
[/math]
-\frac{1}{3e}\simeq-0.123\\
e^{-\frac{1}{3}}\simeq0.717
[/math]
---------------------------------------------------
Punto 2
[math]P\left(1,0\right)[/math]
[math]p:y=ax^2+bx+c[/math]
[math]O \in p \Rightarrow c=0 \Rightarrow y=ax^2+bx[/math]
[math]\text{inoltre } P\in p \Rightarrow 0=a+b \Rightarrow b=-a[/math]
[math]\text{Poiché } f'\left(1\right) =1 \text{ ne segue che la tangente alla parabola in p ha equazione } y=x-1[/math]
[math]\text{Pertanto }[/math]
[math]\left\{ \begin{array}{l}
y = ax^2 - ax \\
y = x - 1
\end{array}
\right.
\quad \Rightarrow \quad
ax^2 - (a+1)x + 1 = 0
[/math]
y = ax^2 - ax \\
y = x - 1
\end{array}
\right.
\quad \Rightarrow \quad
ax^2 - (a+1)x + 1 = 0
[/math]
[math]\text{e quindi}[/math]
[math]\Delta=(a+1)^2-4a=(a-1)^2=0\ \Rightarrow\ a=1[/math]
[math]\text{da cui l'equazione}[/math]
[math]y=x^2-x[/math]
-----------------------------------------------------
Punto 3
[math] R=\int_0^1|x^3\cdot \ln x|\ dx=\lim_{a\to 0^+}\int_a -x^3\cdot ln x\ dx=[/math]
[math]\lim_{a\to 0^+}\left\{\left[\frac{x^4}{4}\ln x\right]_a^1+\int_a^1 \frac{x^4}{4}\cdot \frac{1}{x}\ dx\right\}=[/math]
[math]\lim_{a\to 0^+}\left\{\frac{a^4}{4}\ln a+\int_a^1\frac{x^3}{4}\ dx\right\}=[/math]
[math]\lim_{a\to 0^+}\left\{\frac{a^4}{4}\ln a+\left[\frac{x^4}{16}\right]_a^1\right\}=[/math]
[math]\lim_{a\to 0^+}\left\{\frac{a^4}{4}\ln a+\frac{1}{16}-\frac{a^4}{16}\right\}=\frac{1}{16}[/math]
------------------------------------------------------
Punto 4
Poiché la simmetria rispetto a
[math]x=0[/math]
è data dalle equazioni
[math]\left\{\begin{array}{l}
x'=-x\\ y'=y
\end{array}\right.[/math]
x'=-x\\ y'=y
\end{array}\right.[/math]
si ha per la funzione simmetrica rispetto all'asse y la forma
[math]f_1(x)=-x^3\cdot\ln(-x)[/math]
Poiché la simmetria rispetto a
[math]y=-1[/math]
è data dalle equazioni
[math]\left\{\begin{array}{l}
x'=x\\ y'=-y-2
\end{array}\right.[/math]
x'=x\\ y'=-y-2
\end{array}\right.[/math]
si ha per la funzione simmetrica rispetto a tale retta la forma
[math]f_2(x)=-x^3\cdot\ln(x)-2[/math]
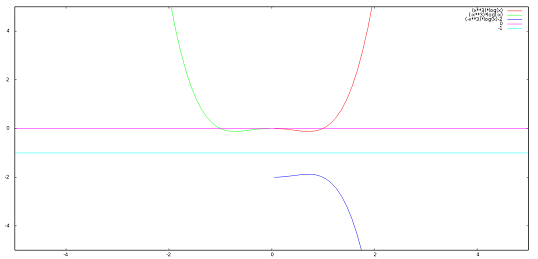
I grafici di tali funzioni sono riportati in figura, dove in rosso, verde e blu sono rappresentate, rispettivamente,
[math]f,\ f_1,\ f-2[/math]
Accedi a tutti gli appunti
Tutor AI: studia meglio e in meno tempo
