vuoi
o PayPal
tutte le volte che vuoi

Ecco qui la soluzione delle tracce di Maturità del 2016 della Seconda prova di maturità del 2016. La soluzione è quella della traccia del secondo problema del liceo scientifico e del liceo delle Scienze applicate.
Seconda prova di Maturità del 2016. Davanti a te il problema di matematica. Il foglio è ancora bianco?
Il primo problema ti sembra impossibile da risolvere? Tranquillo, sei nel posto giusto. Ci siamo qua noi ad aiutarti con il secondo problema di matematica. I nostri tutor si sono impegnati moltissimo nello svolgimento delle soluzioni, ma alla fine ce l’hanno fatta ed ecco qua lo svolgimento del secondo problema di matematica. Avevamo previsto che avreste avuto bisogno del nostro aiuto, e non a caso sei qua a leggere questo articolo. La seconda prova di maturità del 2016 mette in difficoltà i migliori, e non possiamo permettervi di sbagliare il problema della seconda prova maturità 2016. Non ce la siamo proprio sentita di lasciarvi al vostro destino.
Se hai deciso di optare per il secondo problema, ecco qua tutta la soluzione relativa al secondo problema di matematica!
Condizioni iniziali:
per
PUNTO 1
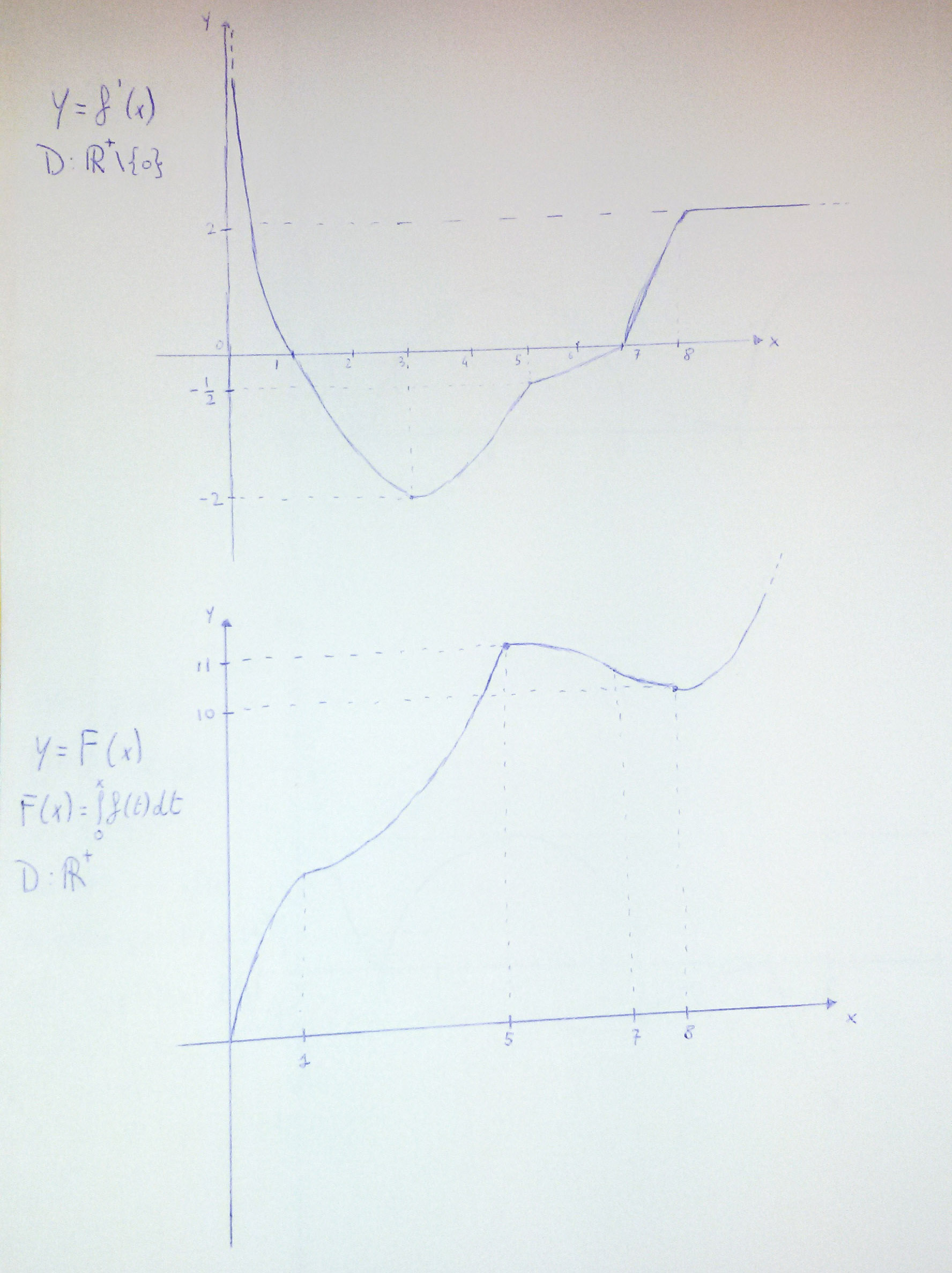
PUNTO 2
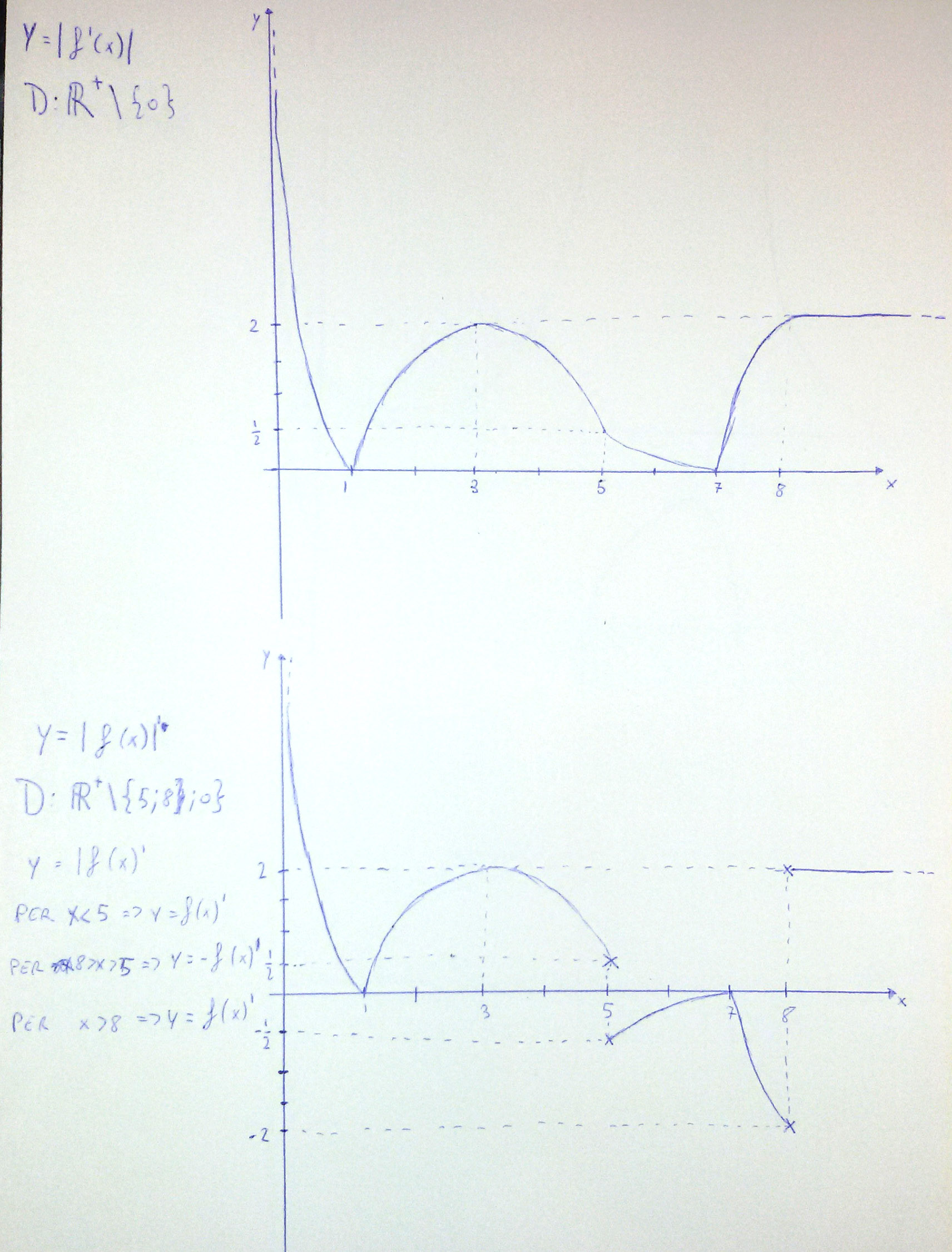
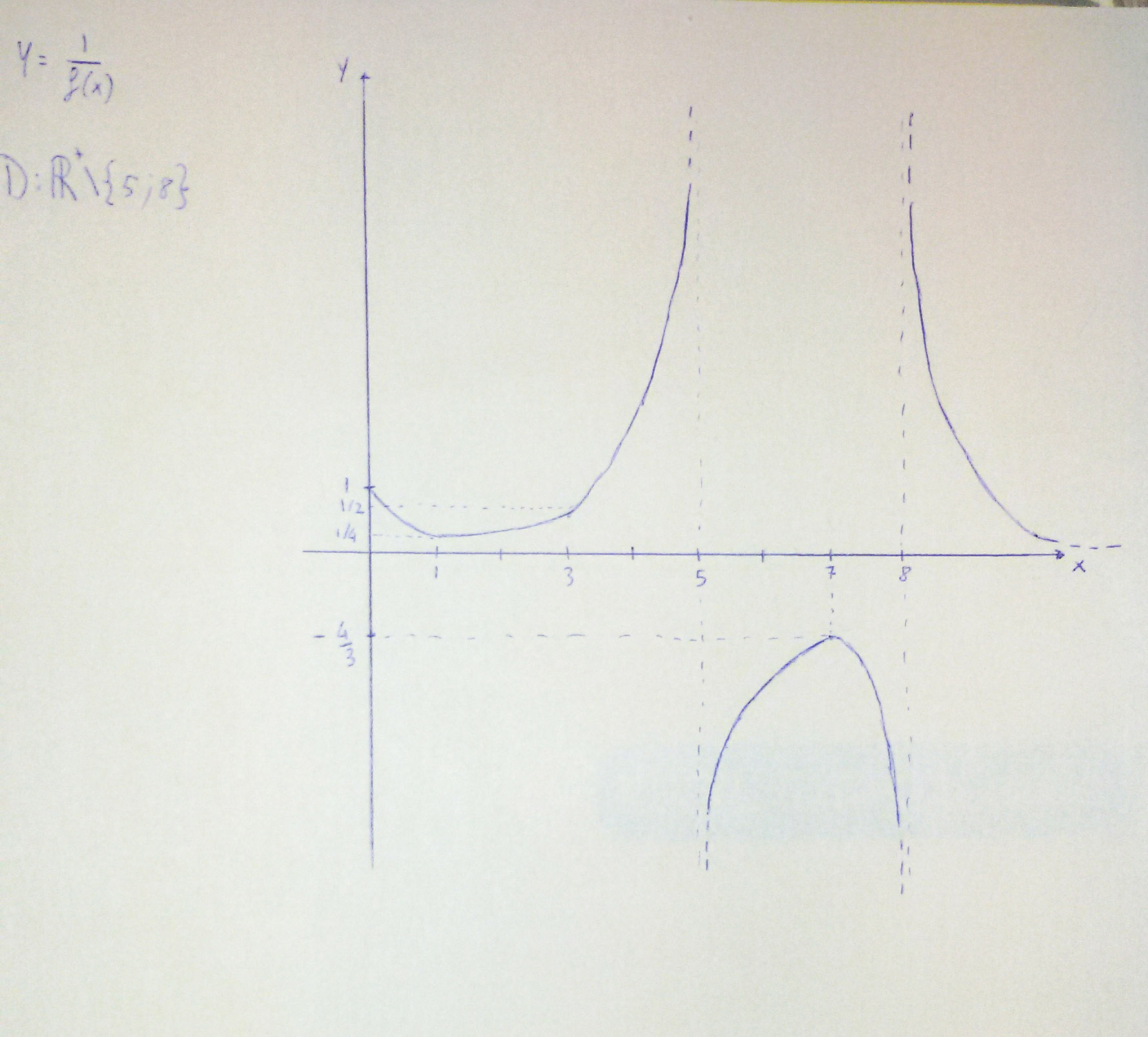
PUNTO 3
Dati:
Per il teorema del valor medio si ha che il valor medio di
Il valore medio di
Il valore medio di
dove si è utilizzato il teorema fondamentale del calcolo integrale per risolvere
Il valore medio di F(x) in [9;10] è
Per
e per il teorema del valore medio, il valor medio di
PUNTO 4
Nel punto
Nel punto
%
Figure 2: La funzione V (z) e V (z) a confronto.
amm
5 16
6 5 6
· −
S(z) = 2 z + z (−z + 1) = 2 z z
6
ed il volume percentuale in funzione di z è:
S(z)·L 16 1
6
−
V (z) = = z z
V 13 6
tot
in cui si intende: 3
·
V = S(1) L = 13m
tot
1.4 Punto 4: obiezione dell’amministratore
L’obiezione mossa dall’amministratore si può riassumere matematicamente ev-
idenziando che egli si aspetta che il volume sia direttamente proporzionale
∝
all’altezza raggiunta dal gasolio ( V (z) z ). Solo in questo caso, infatti,
la quantità percentuale dell’una grandezza coincide con quella della seconda.
3
V (z) ·
z 13 m
3 %
· amm
V (z) = z 13 m =⇒ = = z = V (z)
amm amm
3
V 13 m
tot
Invece l’espressione del volume percentuale V (z) ottenuta al precedente
punto non è direttamente proporzionale a z, come evidenziato dal grafico delle
due funzioni. %
Dove la retta corrisponde a V (z) e la curva a V (z).
amm
L’errore che si commette è la differenza tra le due espressioni percentuali:
16 16 3 8
% 6 6
− − − −
E(z) = V (z) V (z) = z z z = z z
amm 13 13 39
Il suo massimo si calcola imponendo la derivata prima uguale a 0:
1/5
0 3 16 3
5
− ≈
E (z) = z = 0 =⇒ z = 0, 71
err
13 13 16
e verificando che la derivata seconda nel punto è negativa:
00 00
16 16
4 4
− · − · ≈ −0,
E (z) = 5z =⇒ E (z ) = 5(0, 71) 25
err
13 13
2 Secondo Problema
Condizioni iniziali:
f (0) = 1 3
f (1) = 4
f (3) = 2
f (5) = 0 34
−
f (7) =
f (8) = 0
f (10) = 4 0
f (x) = +∞
lim +
x7→ 0
0 12
−
f (5) = poichè è il valore del coefficiente angolare della retta tangente al
grafico in x = 5
0 −2poichè
f (3) = è il valore del coefficiente angolare della retta tangente al
grafico in x = 3 0
≥
per x 8 : f (x) = 2
0 0
f (1) = f (7) = 0 poichè sono punti di min/max relativo
00
f (3) = 0 poichè è un punto di flesso
2.1 Punto 1
2.2 Punto 2
2.3 Punto 3
Dati:
5
R f (x)dx = 11
0 8
R
| f (x)dx = 1|
5
Per il teorema del valor medio si ha che il valor medio di f (x) nell’intervallo
[0; 8] è 5 8
8 R R
R f (x)dx+ f (x)dx
f (x)dx 11−1 5
= = =
0 5
0 8−0 8 8 4
|f
Il valore medio di (x)| in [0; 8] è
8 5 8
R R R
|f |f |f
(x)|dx (x)|dx+ (x)|dx 11+1 3
= = =
0 0 5
8−0 8 8 2
0
Il valore medio di f (x) in [1; 7] è
0
7 −3
R −4
f (x)dx f (7)−f (1) −19
= = =
1 4
7−1 6 6 24
dove si è utilizzato il teorema fondamentale del calcolo integrale per risolvere
0
R f (x)dx.
Il valore medio di F(x) in [9;10] è
5 8
R R
F (8) = f (x)dx + f (x)dx = 10
0 5 x x 2
R R
≥ − −
Per x 8 si ha F (x) = 10 + f (x)dx = 10 + (2x 16)dx = x 16x + 74
8 8
e per il teorema del valore medio, il valor medio di F (x) nell’intervallo [9, 10]
vale: 10
h i
10 3
x 37
2 2
R − −
F = x 16x + 74 dx = 8x + 74x =
3 3
9 9
2.4 Punto 4
Nel punto x = 8 la F (x) ha un minimo relativo. Dunque la retta tangente ha
coefficiente angolare pari a 0, e la sua equazione risulta facilmente:
y = F (8) = 10 0
Nel punto x = 0 abbiamo: m = F (0) = f (0) = 1 da cui l’equazione della
tangente:
y = x + q per determinare q impongo il passaggio dal punto (0,0)
4
Figure 3: Soluzione del secondo punto - 1.
5
Figure 4: Soluzione del primo punto - 2.
6
Figure 5: Soluzione del secondo punto.
7
Figure 6: Quesito 2.
0 = q dunque abbiamo determinato l’equazione della retta tangente ad F(x)
nel punto x=0:
y = x
3 Quesiti
3.1 Quesito 1
√
+∞ 2
−x
R e dx = π
−∞ ∪ 2
−x
R e dx = 1
−∞ +∞
2 2
−x −x
R ' ∪
Poiché e è una funzione pari, e e dx 1, 77, allora deve
−∞
1,77 .
essere positivo dato che 1 è maggiore di 2
∪ 2
−x
7
R
A = x e dx = 0 Poiché la funzione integranda è dispari.
−∪
∪ ∪ −∪ +∞
2 2 2 2
−x −x −x −x
R R R R
− −
B = e dx = e dx e dx = 1 e dx =
−∪ −∞ −∞ ∪
√
√ − −
− π 1) = 2 π
1 ( +∞ 2
−5x
R
C = e dx
−∞ √
+∞ 2
−x
R π si ricava che
Ricordiamo che dall’integrale di Gauss e dx =
−∞
√
+∞ 2 π
−x a
R (e ) dx = √
−∞ a √
+∞ 2 π
−5x
R
Allora e dx = √
−∞ 5
3.2 Quesito 2
2
−
y = 1 ax a¿0
b ∆
−
V (− , ) V (0, 1)
2a 4a
( (
y = k y = k
2 2
− −
1 ax = k 1 ax = y
8
q 1−k
±
x a q 1−k
base rettangolo = 2 a
altezza rettangolo = k
q 1−k
Area rettangolo = 2k a
q 1−k
Perimetro rettangolo = 4 + 2k
a
Massimizziamo l’area: √
√
q 2(1−k)−ak
k a
1−k
2
2k
1−k √
− − = =0
=
2 √ √ √
√
a a
1−k 1−k a 1−k
2 a
− −
2 2k ak = 0
k(a + 2) = 2]
2
k = Sostituisco questo valore di k nel perimetro
2+a √
q 2
1− 2+a+4
4
4 4 4
2+a
Perimetro rettangolo = 4 + = + = =
√
a 2+a 2+a 2+a
2+a
√
4( 2+a+1)
2+a
Massimizziamo il perimetro:
√
42 √
6 (2+a)−4( 2+a+1)
√ −2 2+a−4
6 2 2+a = =0
2 2
(2+a) (2+a)
√
−2 −
2 + a 4 = 0
√ −2
2 + a =
2+ a =4
a =2
3.3 Quesito 3 b +2 3
x
2 2 2 2 2 3
R R −
− −
Volume sfera = π [f (x)] dx = π ] = π(r
(r x )dx = π[r x −2
−2 3
a
3 3
r r 43
3 3
−
+ r ) = πr
3 3 3
h−r 3 (h−r )
h−r
x 2 3
2 2 2
R − −
− −
π ] = π[r h r ]
(r x )dx = π[r x 0
3 3
0 4 2
3 3
·
πr , il volume di metà sfera 4πr e il
Sottraendo dal volume totale 3 3
volume ricevuto prima, otteniamo:
3
h
2
· −
Volume calotta = π (2h )
3
3.4 Quesito 4
10 domande
4 risposte a domande
1 risposta esatta per ogni domanda
A = ”Rispondere almeno a otto domande”
P(A) = ?
P(A) = P(0 errori) + P(1 errore) + P(2 errori)
14 10
)
P (0 errori) = ( n 34 14
9
·
P (1 errore) = ( ) ( )
1
n 34 14
2 8
·
P (2 errori) = ( ) ( )
2
10 9 10
1 34 14 3 1
2 8
· · ·
P (A) = + 10 + ( ) ( ) =
4 2 4 4
1 14 15 1 3
8 2 2
( ) [( ) + ( ) + 45( ) ]
4 2 4 4
∼
109 0, 000416
=
262144 9
3.5 Quesito 5
K(−2, 1, 2) P ? punto di tangenza
− −
π : 2x 2y + z 9 = 0
Vettore di parametri direttori del piano π
− − − −
V = P K = [x x , y y , z z ]
p k p k p k
− −
= [x + 2, y 1, z 2]
p p p
Sostituiamo parametri direttori di V in π :
· − · − ·
(x + 2) x + (y 1) y + (z 2) z + d = 0
p p p
x + 2 = 2
p
− −2
y 1 = Per l’equazione data di π
p −
z 2 = 1
p
x = 0
p −1 −1,
y = P (0, 3) punto tangenza
p
z = 3
p
P K = raggio
p 2 2 2
− − −
r = (x x ) + (y y ) + (z z ) =
p k p k p k
√
p 2 2 2
− −
(0 + 2) + (−1 1) + (2 3) = 4 + 4 + 1 = 3
3.6 Quesito 6 −3
∃P |P − ≤ ∀
(x)| (x) cos x| 10 x R
n n−1 6
Poiché P (x) = a x + a x + ... +a , a = 0
n n−1 0 n
≥ ±∞
con a , ... , a e n 1, a seconda del segno di a lim P (x) =
R
n 0 n x→∞
−3
|P − ≤ ∀
In entrambi i casi (x) cos x| non può essere 10 x + R
Nel caso limite che P (x) = a = cost,
0 −3
|P − |a − 6 ∀
(x) cos x| = cos x| non può essere = 10 x oscillando il
R
0
cos x tra -1 e 1 periodicamente.
3.7 Quesito 7
Ci stiamo chiedendo quale è la probabilità che la pedina passi per B (in posizione
(3,5)) in uno dei percorsi che vanno da O(0,0) ad A (in posizione (7,7)). Quindi
sarebbe la probabilità di passare in B sapendo che sono andato da O ad A in
14 passi.
Considero i percorsi totali per A in 14 passi NOTA: Posso arrivare in A solo
in 14 passi, perché 7+7=14.
14 14!
=
7 7!7!
I percorsi totali per B (in 8 passi perché 3+5=8
8 8!
=
3 3!5!
Se sono in B, i percorsi totali da B ad A in 6* passi saranno:
6! = 15
4!2!
*una volta che sono arrivato in B posso considerarla la nuova origine, rispetto
alla quale il punto A è in posizione (4,2)
Per determinare tutti i percorsi che arrivano ad A passando per B, quindi,
basta fare:
7!7! 8! ≈
15 0, 245
14! 3!5! 10
3.8 Quesito 8
→
f (x) : R R
x 2
f (x) = e (2x + x )
Si cerca la primitiva di f (x) passante per (1, 2e)
R
g(x) = f (x)dx ; g(1) = 2e
x 2 x
R R
g(x) = 2xe dx + x e dx
x x x x x
R R
− −
2xe dx = 2xe 2e dx = 2xe 2e
2 x 2 x x 2 x x x
R R
− −
x e dx = x e 2xe dx = x e 2xe + 2e
x x 2 x x x 2 x
− 6 − 6 6
g(x) = (6 2xe 2e ) + (x e 2xe + 2e ) + C = x e + C
→ →
g(1) = 2e e + C = 2e C = e
2 x
g(x) = x e + e
3.9 Quesito 9
x= t
r : y = 2t
z= t
( −
x+ y + z 3=0
S : −
2x y = 0
P (1,0,-2)
(1,2,1) vettore direttore di r
Trasformo s dalla forma cartesiana a parametrica:
( − −
x=3 y z
S : − − −
2(3 y z) y = 0
( − −
x=3 y z
− − −
6 2y 2z y = 0
( − −
x=3 y z
−3y
2z = + 6
( − −
x=3 y z
3
− y
z = 3 2
12 32
−
(− , 1, ) vettore direttore di S
Date due rette con parametri direttori:
(l , m , n ) e ((l , m , n )∃π che soddisfa le nostre condizioni. Possiamo
1 1 1 2 2 2
calcolare l’equazione cartesiana grazie all’annullamento delle determinanti di
questa specifica matrice:
− − −
x x y y z z
0 0 0
A l m n
= con x , y , z coordinate del punto P
1 1 1 0 0 0
l m n
2 2 2
−
x 1 y z +2
− −
y z +2 x 1 z +2 x 1 y
A − −
1 2 1
= = +2 =
32
32 1 12
−
− − − 1
1
1 3
− − 2
1
2 2
3 32 3 12 12
−(− − − − −
= y z 2) + 2(− x + + z + 1) (x 1 + y) =
2 2
32 1
− − −
= y + z + 2 3x + 3 + z + 2 x + 1 y
2
−4x
= + y + 2z + 8
−4x
π : + y + 2z + 8 = 0 11







 Accedi a tutti gli appunti
Accedi a tutti gli appunti
 Tutor AI: studia meglio e in meno tempo
Tutor AI: studia meglio e in meno tempo









