
Prepararsi con anticipo all' esame di maturità del liceo scientifico è fondamentale. Dunque, perchè non esercitarsi con il calcolo combinatorio senza ripetizione? Il prof di matematica, Francesco Bologna, ci spiega come affrontare tale quesito di matematica sia con il metodo tradizionale, sia con l'aiuto di una delle calcolatrici scientifiche più diffuse, la Casio FX991ES PLUS.
Scopri tutte le tracce della maturità scientifica degli anni passati
Impara ad usare la calcolatrice, guarda il nostro video!
CALCOLO COMBINATORIO SENZA RIPETIZIONE
Le indicazioni nazionali riguardanti gli obiettivi specifici di apprendimento dell'allievo del liceo hanno previsto che, al termine del percorso liceale, lo studente dovrà conoscere i concetti salienti relativi al calcolo delle probabilità e dell'analisi statistica.
In particolare tra gli obiettivi specifici di apprendimento viene dato risalto al paragrafo "Dati e previsioni" nel quale viene esplicitato che l'allievo dovrà saper distinguere tra caratteri qualitativi, quantitativi discreti e quantitativi continui, operare con distribuzioni di frequenze e rappresentarle.
Dovrà, inoltre, aver assimilato le definizioni e le proprietà dei valori medi e delle misure di variabilità, saper ricavare semplici inferenze, nonchè l'uso strumenti di calcolo (calcolatrice, foglio di calcolo) per analizzare raccolte di dati e serie statistiche.
Nel secondo biennio e nell'ultimo anno, in ambiti via via più complessi, l'allievo dovrà acquisire i concetti relativi alle distribuzioni doppie condizionate e marginali, alla deviazione standard, dipendenza, correlazione e regressione, e di campione.
Studierà la probabilità condizionata e composta, la formula di Bayes e le sue applicazioni, nonchè gli elementi di base del calcolo combinatorio, concludendo con lo studio di alcune distribuzioni discrete
e continue di probabilità (come la distribuzione binomiale, la distribuzione normale, la distribuzione di Poisson).
In questo paragrafo affrontiamo l'analisi del calcolo combinatorio senza ripetizione.
CALCOLO COMBINATORIO SENZA RIPETIZIONE
Il calcolo combinatorio studia i modi di combinare gli elementi di un insieme fissati alcuni criteri. L'obiettivo è quello di stabilire quanti gruppi si possono formare da una famiglia di oggetti. I gruppi
possono differire per l'ordine degli elementi ( permutazioni -
) per la presenza o meno di un elemento
( combinazioni -
), o per entrambe le caratteristiche ( disposizioni -
).
Le combinazioni si distinguono in semplici e con ripetizione.
Analizziamo le prime.
Esercizi:
-
1. Quanti sono gli anagrammi della parola "amore"?
2. Da una classe di 24 allievi in quanti modi si possono scegliere 3 rappresentanti?
3. Quanti sono i numeri con tre cifre diverse che si possono formare con le cifre 1, 2, 3 e 4?
Esercizio 1. Quanti sono gli anagrammi della parola "amore"?
Gli anagrammi sono un esempio tipico di permutazioni semplici di
elementi.
Il numero di permutazioni è calcolato tramite la relazione:
P_n=n\left(n-1\right)\bullet{}\left(n-2\right)\bullet{}1=n!
[/math]
Quindi nel nostro caso
si avrà:
2. Da una classe di 24 allievi in quanti modi si possono scegliere 3 rappresentanti?
Il numero di combinazioni è calcolato tramite la relazione:
Quindi nel nostro caso
e
si avrà:
3. Quanti sono i numeri con tre cifre diverse che si possono formare con le cifre 1, 2, 3 e 4?
Il numero di disposizioni è calcolato tramite la relazione:
Quindi nel nostro caso
e
si avrà:
Vediamo come la calcolatrice FX991ES+ può rendere la procedura di calcolo molto semplice.

ESERCIZIO 1
Passaggio #1
Attraverso al combinazione:
Collochiamoci nel menù COMP
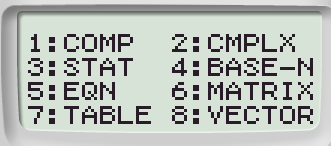
Passaggio #2
Digitiamo
Per eseguire il calcolo del numero di permutazioni:
.png)
.png)
Passaggio #3
Tramite il tasto cursore inseriamo i valori:
-scheda7-esercizio-2.png)
Digitando = otterremo il valore cercato.
.png)
ESERCIZIO 2
Passaggio #1
Attraverso al combinazione:
Collochiamoci nel menù COMP

Passaggio #2
Digitiamo
Per eseguire il calcolo del numero di combinazioni:
-scheda7-esercizio-2.png)
-scheda7-esercizio-2.png)
Passaggio #3
Tramite il tasto cursore inseriamo i valori:
-scheda7-esercizio-2.png)
Digitando = otterremo il valore cercato
-scheda7-esercizio-2.png)
ESERCIZIO 3
Passaggio #1
Attraverso al combinazione:
Collochiamoci nel menù COMP

Passaggio #2
Come visto in precedenza, digitiamo
Per eseguire il calcolo del numero di permutazioni:
.png)
per eseguire il calcolo del numero di combinazioni:
-scheda7-esercizio-2.png)

Passaggio #3
Tramite il tasto cursore inseriamo i valori:
-scheda7-esercizio-2.png)
Digitando = otterremo il valore cercato.
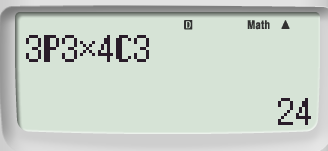






 Accedi a tutti gli appunti
Accedi a tutti gli appunti
 Tutor AI: studia meglio e in meno tempo
Tutor AI: studia meglio e in meno tempo