Tutte le cose che si conoscono hanno un numero [Pitagora]

A Pitagora è attribuito il pensiero: "Tutte le cose che si conoscono hanno un numero; senza quello nulla sarebbe possibile conoscere né sapere". Ricordo con molta stima e simpatia un direttore della pianificazione e controllo che aveva una grande fiducia nei numeri del conto economico di un'impresa. Per ciascuna area di businness e per ogni semestre, faceva calcolare l'incidenza dei costi (lavoro, materiali, appalti, diversi), degli ammortamenti, degli oneri e degli utili e delle imposte sui ricavi.
Chiamava queste tabelle matrici delle percentuali e riteneva che ciascun valore dovesse mantenersi entro certi limiti per uno sviluppo sano dell'azienda.
A noi giovani (un economista, due ingegneri, uno statistico ed un perito informatico) aveva dato, tra l'altro, il compito di investigare se queste percentuali dovessero avere, come lui pensava, un valore ottimale per l'equilibrio dell'impresa.

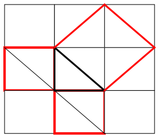
Terne pitagoriche erano già note ai babilonesi (Es. 3,4,5) e agli indiani (Es. 5,12,13), ma Pitagora ebbe il merito di generalizzare il problema (anche se non è certo che dette dimostrazione del suo teorema) per valori qualunque dei cateti e dell'ipotenusa di un triangolo rettangolo.
Se i cateti valgono 1 l'ipotenusa vale radice di 2: pare che così sia venuto fuori lo scandalo dei numeri irrazionali.
Con Pitagora iniziò a prevalere l'idea che la matematica dovesse rivolgersi alla conoscenza pura in contrapposizione alla concezione pratica ed applicativa che ne avevano avuto gli Egizi e i Babilonesi.
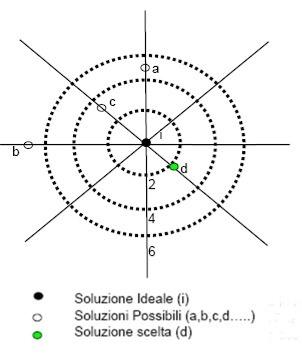
Il concetto di distanza tra due punti in uno spazio ad n dimensioni è strettamente collegato al teorema di Pitagora ed esso è fondamentale per molti problemi decisionali e gestionali delle organizzazioni: dalle scelte con criteri multipli, al controllo di qualità, al filtro di Kalmann per la guida e il controllo dei sistemi robotizzati.