Correlazione tra i punti di un grafico

In numerose attività si effettuano misure sperimentali: campi coltivati, foreste, corsi d'acqua, laboratori, impianti, fabbriche Si fanno indagini economiche, rilevazioni di mercato e di numerosi fenomeni sociali. Tutte sono fonti di dati, che richiedono elaborazioni per fornire indicazioni utili a comprendere i fenomeni osservati, trarre conclusioni, orientare analisi successive e/o decisioni.
Nel caso pi comune ci si ritrova per le mani una tabella di valori x, y. La prima domanda che ci si pone : Esiste un legame tra queste due variabili?

È pratica normale tracciare un semplice diagramma per punti delle coppie di valori x, y. Questo già ci fa capire grossolanamente se esiste una correlazione. Se ci troviamo una nuvola di punti (fig. 1) difficilmente penseremo che esista correlazione.



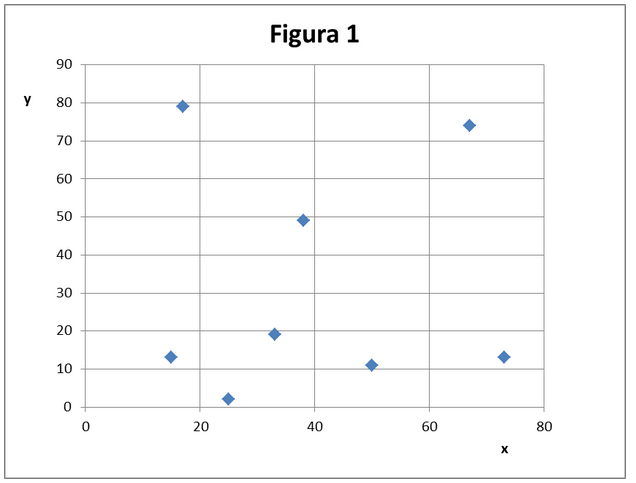
In altri casi, come da fig. 2 vien da pensare che si possa tirare una linea che passa tra i punti, a patto di trascurare il secondo punto(18,60) che pare proprio un pesce fuor dacqua: lo definiamo outlier e lo scartiamo. Poi tracciamo, anche a mano, una linea che chiameremo curva di fitting. E una prassi che si sempre seguita e funziona per gran parte degli scopi pratici. Da quando hanno inventato i calcolatori (ed i PC) si iniziato ad applicare semplici metodologie per tracciare con maggiore precisione la linea interpolante. Si determinano i parametri della linea minimizzando la somma degli scarti quadratici tra il valore di y misurato ed il quello predetto dalla curva di fitting. Essa contiene due parametri: a =intercetta, b= pendenza.
E si calcola qualche indice statistico che ci permetta di stabilire con quale precisione ed affidabilit possiamo accettare la linea interpolante.



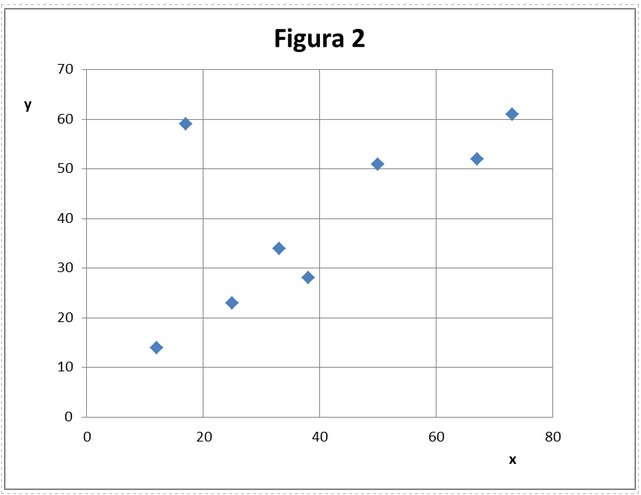
Torniamo ora al punto iniziale di questo documento. In assenza di qualunque teoria o informazione pregressa che colleghi le due variabili x ed y, la prima domanda da porre Esiste correlazione? Risposta: Forse. Ulteriore domanda: Quale tipo di correlazione?. Risposta: Ipotizziamo la pi semplice, ossia una correlazione lineare.
Correlazione lineare equivale a dire che esiste una retta interpolante: y = a+bx.
Bene, l'indice statistico che si usa in questo caso si definisce Coefficiente di correlazione lineare(r).

Se usiamo EXCEL non ci stiamo a preoccupare di fare calcoli, basta usare la funzione CORRELAZIONE().
Tale coefficiente un numero compreso in un intervallo: -1 < r < 1.

Il valore di r è positivo quando la correlazione è positiva (y è funzione crescente di x), negativa quando è negativa (y decresce al crescere di x). La correlazione è perfetta quando r = 1. Non esiste alcun tipo di correlazione tra le due variabili quando r = 0.

Consideriamo, per fissare le idee che la correlazione nel nostro esperimento sia positiva (quindi r > 0). Quando r ha un valore elevato, diciamo 0,8 < r < 1, la correlazione è forte e la retta interpolante è molto precisa, ossia comporta piccoli errori. Questo caso si verifica spesso quando si fanno misure di grandezze fisiche o chimiche in laboratori ben organizzati. Pianificando bene il piano sperimentale con metodologie ben note e avvalendosi di strumenti di qualit e ben calibrati, si riesce a rendere abbastanza piccolo l'errore sperimentale. Spesso le prove si possono fare e rifare in numero adeguato, se i tempi ed i costi lo permettono, scartando quelle che paiono dare risultati fuori campo o comunque obiettivamente sospette.

Esistono tuttavia altre situazioni molto più complesse dove non si riesce ad evitare notevoli effetti di disturbo di variabili esogene. Gli strumenti di misura non sono molto efficienti e non si possono migliorare. Oppure anche il tipo di rilevazione avviene sotto condizioni di prova non controllabili. Oppure non si possono rifare le prove: quello che è fatto è fatto, anche se non molto soddisfacente. Tipicamente, nel caso di misure biologiche, econometriche, sociologiche.

In diversi casi non si sa bene se y dipende effettivamente da x. In questi casi non facili si calcola comunque il coefficiente r per tentare di decidere in proposito. E spesso si ottengono valori di r piuttosto bassi: 0,5, 0,4, 0,3. Con tali valori possiamo avere dei dubbi. Può essere che decidiamo di assumere che la correlazione esista quando non vero: i dati sperimentali, affetti da errore, ci hanno ingannato.

In questi casi capziosi necessario ricorrere alla statistica, per il tramite di un test sul coefficiente di correlazione.

Prima di presentarlo facciamo una precisazione: le misure che noi abbiamo fatto, costituite da N prove, rappresentano un campione. E dunque il coefficiente r una stima campionaria. Se potessimo ripetere all'infinito le misure otterremmo il coefficiente di correlazione della popolazione, che per convenzione si rappresenta con la variabile ?. Dunque ? il valore vero, ma inconoscibile, che definisce la correlazione, mentre r solo un stima di ?, non sappiamo quanto precisa.

Bene, gli statistici ci dicono che la variabile casuale segue la distribuzione statistica del t di Student (*), con un numero di gradi di libertà v = N 2. La distribuzione del t di notevole importanza. La sua descrizione e le relative tavole si trovano in qualunque libro di statistica. La troviamo anche su EXCEL con la funzione INVT() (**).

Se continuiamo ad assumere che la correlazione x, y sia positiva, il test sulla correlazione lineare si formula in questi termini:

Ipotesi H0: si assume che sia ? = 0 (vale a dire non esiste alcuna correlazione tra x ed y)

Ipotesi H1(alternativa): si assume che sia ? > 0 (vale a dire esiste correlazione positiva tra x ed y)

Decisione: assunto un livello di significatività (rischio) ?, si trova sulla tavola del t il valore t (v ,1- ?), vale a dire il valore delle distribuzione t con v gradi di libertà e probabilità 1- ?.

Se risulta:



In altre parole, se il t calcolato pi grande del t teorico, si respinge l'ipotesi H0 e dunque si tende ad accettare l'ipotesi H1. Viceversa nel caso contrario (***).

Gli esempi riportati nel file EXCEL allegato ci presentano diverse situazioni.
L'esempio 1 è un tipico risultato di prove di laboratorio molto accurate. Il diagramma dei dati sperimentali ci rivela immediatamente una correlazione lineare ben definita. L'analisi statistica fornisce i valori i parametri a e b della retta ed il valore di r. Il test mostra che = è di gran lunga maggiore del t teorico della distribuzione di Student. Non avevamo dubbi ed ora siamo convinti. La correlazione sicura.
Ben diverso il caso dell esempio 2. Abbiamo una nuvola di punti. Proviamo a tracciare con EXCEL la retta di regressione (linea di tendenza): rivela una tendenza positiva. Ma gli errori sperimentali sono grandi. Il coefficiente di correlazione (0,53) non è entusiasmante ma neppure trascurabile. Qui ci vuole davvero il test di ipotesi. Il quale rivela che la correlazione non statisticamente significativa. Dobbiamo quindi concludere che non esiste correlazione tra le due variabili.

Vediamo ora l'esempio 3, riportato di seguito.



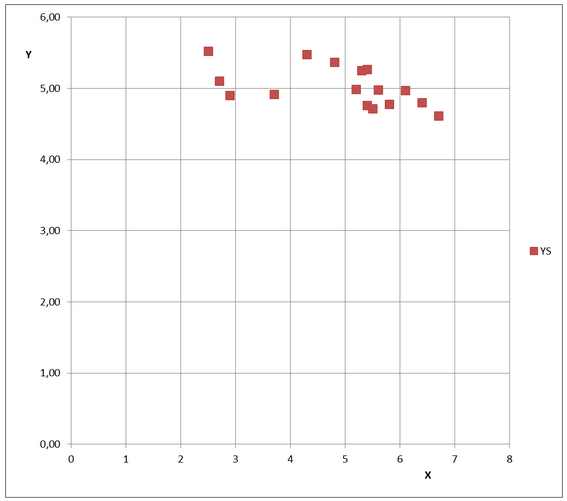
La dispersione dei dati è limitata( piccoli errori sperimentali) ma non è immediato decidere a occhio se la correlazione positiva o negativa. Si ottiene r= -0.51,
Ipotesi H0: si assume che sia ? = 0 (vale a dire non esiste alcuna correlazione tra x ed y)

Ipotesi H1(alternativa): si assume che sia ? # 0 (vale a dire esiste correlazione positiva o negativa tra x ed y)

Il test di ipotesi viene formulato in questo modo:




Si noti che è stato assunto il valore assoluto del t calcolato, perché esso potrebbe essere negativo. Inoltre il test, in questo caso a due code e l'area di ciascuna coda vale ?/2. Come riportato nel file EXCEL (SHEET Esempio 3) la (2) soddisfatta e quindi la correlazione risulta statisticamente significativa.

Infine facciamo un piccolo confronto tra i risultati statistici degli esempi 2 e 3:

	Coefficiente di corr. lineare	Risultato t test
ESEMPIO 2	0,53	Non esiste correlazione
ESEMPIO 3	-0,51	Esiste correlazione(negativa)

I coefficienti sono in valore assoluto- quasi uguali, ma i test di ipotesi portano a conclusioni ben diverse.

Si può dunque concludere che, in generale, il solo calcolo del coefficiente di correlazione non basta e deve essere accompagnato dal test statistico.

CONCLUSIONE

In questo articolo stato presentato il coefficiente di correlazione lineare r, corredato dal suo test di ipotesi, come metodo semplice ed efficace per accertare l'esistenza di una correlazione lineare statisticamente significativa tra le variabili x,y.
Esistono approcci matematico-statistici di tipo pi complesso applicabili nell'analisi della regressione lineare (di cui la retta solo un semplice esempio), che determinano la validità del modello di regressione ipotizzato, mediante la distribuzione F di Fisher ed inoltre stimano probabilità e limiti di fiducia dei parametri del modello ricorrendo al t di Student.

APPENDICE

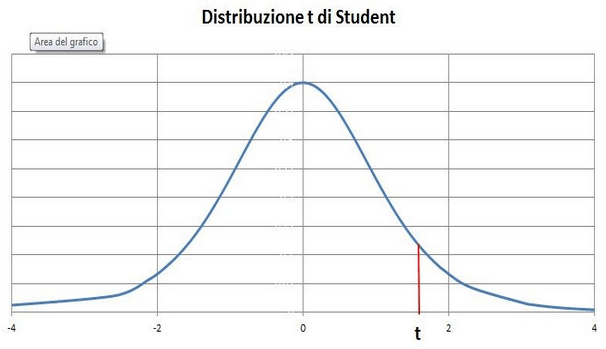
La distribuzione del t di Student(figura sotto), relativa ai piccoli campioni ( N < 30) una curva simmetrica. L'area sotto la curva ( l'integrale da -? a +?) vale 1 (o, che lo stesso, 100%). Mentre l'area dell intervallo compreso tra -? e t (individuato dal segmento rosso nella figura sotto) rappresenta il valore 1 - ? , ossia la probabilità di prendere una decisione corretta respingendo l'ipotesi H0. Pertanto, se risulta si respinge ipotesi H0 con 1-? probabilità di non sbagliare. La zona sotto la curva a destra del t si chiama coda ed la sua area vale ?, detto livello di significativit; rappresenta la probabilit di sbagliare quando, essendo respingiamo l'ipotesi H0. Abitualmente si fissa il livello ? = 5%, quindi risulta 1-? = 95%.

Note

(*) Student lo pseudonimo dell'inventore della distribuzione: William Gossett. Per la descrizione di questa statistica ed una tabella dei suoi valori: http://it.wikipedia.org/wiki/Distribuzione_t_di_Student
(**) Excel ci permette di calcolare anche i parametri a e b della retta interpolante, rispettivamente con le funzioni INTERCETTA () e PENDENZA ()
(***) Il linguaggio e le notazioni sopra riportate per i test statistici sono alquanto ostici e non facili da digerire. Ma tant. Gli statistici li hanno definiti in questo modo con validi motivi. E conveniente imparare ad usarli.