Geometria analitica: Il triangolo hat{ABC} ha per vertici A(1;3); B(1/2;3/2); C(2;1).Verificare che l triangolo è is

di francesco.speciale

Ominide

2 min. di lettura

Vota

Il triangolo

[math]hat{ABC}[/math]

ha per vertici

[math]A(1;3); B(1/2;3/2); C(2;1)[/math]

.Verificare che l triangolo è isoscele
e determinre le misure del perimetro e dell'aria.

Svolgimento

Per perimetro si intende la somma dei segmenti

[math]ar(AB), ar(BC), ar(AC)[/math]

.
Quindi calcoliamo le misure dei seguenti segmenti:

[math]ar(AB)=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}=\sqrt((1/2-1)^2+(3/2-3)^2)=\sqrt((-1/2)^2+((3-6)/2)^2)=\sqrt(1/4+(-3/2)^2)=[/math]

[math]=\sqrt{1/4+9/4}=\sqrt((10)/4)=1/2\sqrt(10)[/math]

[math]ar(AC)=\sqrt{(x_3-x_1)^2+(y_3-y_1)^2}=\sqrt((2-1)^2+(1-3)^2)=\sqrt(1+4)=\sqrt5[/math]

[math]ar(BC)=\sqrt{(x_3-x_2)^2+(y_3-y_2)^2}=\sqrt((2-1/2)^2+(1-3/2)^2)=\sqrt(((4-1)/2)^2+((2-3)/2)^2)=[/math]

[math]=\sqrt{(3/2)^2+(-1/2)^2}=\sqrt(9/4+1/4)=\sqrt((10)/4)=1/2\sqrt(10)[/math]

Pertanto

[math]2p=ar(AB)+ar(BC)+ar(AC)=\sqrt5+1/2\sqrt{10}+1/2\sqrt{10}=\sqrt5+\sqrt{10}=\sqrt5(\sqrt2+1)[/math]

Inoltre possiamo ire che il triangolo

[math]hat{ABC}[/math]

è isoscele, poichè

[math]ar{AB}=ar{BC}[/math]

.
Pertanto

[math]ar{AC}[/math]

sarà la base del triangolo.
Lìarea del riangolo è data dalla formula:

[math]A=(b \cdot h)/2[/math]

.
Dobbiamo calcolare l'altezza, cioè il segmento avente come uno dei vertici il punto

[math]B[/math]

e come secondo vertice il punto medio del segmento

[math]ar{AC}[/math]

.
Calcoliamo il punto medio, che indicheremo con

[math]M[/math]

, del segmento

[math]ar{AC}[/math]

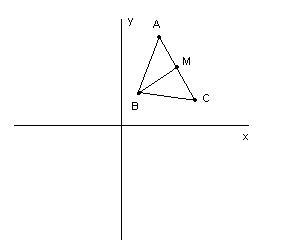
Le coordinate del punto medio di un segmento sono le semisomme (medie aritmetiche)
delle coordinate omonime degli estremi.
In formule

[math]x_M=(x_2+x_1)/2 ^^ y_M=(y_2+y_1)/2[/math]

.
Nel nostro caso, si ha:

[math]x_M=(1+2)/2=3/2 ^^ y_M=(3+1)/2=2[/math]

.
Quindi il punto medio sarà

[math]M(3/2;2)[/math]

Calcoliamo quindi la misura del segmento

[math]ar{BM}[/math]

[math]ar(BM)=\sqrt{(x_M-x_2)^2+(y_M-y_2)^2}=\sqrt((3/2-1/2)^2+(2-3/2)^2)=\sqrt((2)^2+((4-3)/2)^2)=[/math]

[math]=\sqrt{4+1/4}=\sqrt((4+1)/4)=\sqrt(5/4)=1/2\sqrt5[/math]

.
Pertanto

[math]A=(b \cdot h)/2=((ar{AC}) \cdot (ar{BM}))/2=(\sqrt5 \cdot 1/2\sqrt5)/2=5/4=1,25[/math]

Geometria analitica: Il triangolo hat{ABC} ha per vertici A(1;3); B(1/2;3/2); C(2;1).Verificare che l triangolo è is

Il triangolo hat{ABC} ha per vertici A(1;3); B(1/2;3/2); C(2;1).Verificare che l triangolo è isoscele e determinre le misure del perimetro e dell'aria. Svolgimento Per perimetro si intende l...

Recensioni

Domande e risposte

Help (321322)

Aiuto urgente per compiti

Problema con potenze

I migliori insegnanti di Matematica

Giovanni C.

Salvatore F.

Appunti correlati

Geometria analitica: Verificare che il triangolo di vertici A(3;2); B(6;1); C(5;4) è isoscele.

Geometria analitica: Verificare che il triangolo di vertici A(4;0); B(0;3); C(1;-4) è isoscele.

Geometria analitica: Verificare che il triangolo di vertici A(3;0); B(-3;0); C(0;-3sqrt3) è equilatero.

Dato il triangolo di vertici A(0,3) B(2,3) C(6,1) verificare che il perimetro è doppio di quello con vertici i punti medi

Recensioni

Domande e risposte

Help (321322)

Aiuto urgente per compiti

Problema con potenze

I migliori insegnanti di Matematica

Giovanni C.

Salvatore F.