Verificare che il triangolo di vertici
[math]A(3;0); B(-3;0); C(0;-3\sqrt3)[/math]
è equilatero. Svolgimento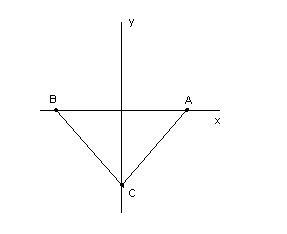
Dobbiamo dimostrare che i tre lati sono uguali tra loro.
Calcoliamo le misure dei tre segmenti
[math]ar(AB)=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}=\sqrt((-3-3)^2+(0-0)^2)=\sqrt(36)=6[/math]
[math]ar(AC)=\sqrt{(x_3-x_1)^2+(y_3-y_1)^2}=\sqrt((0-3)^2+(-3\sqrt3-0)^2)=\sqrt(9+(9 \cdot 3))=\sqrt(36)=6[/math]
[math]ar(BC)=\sqrt{(x_3-x_2)^2+(y_3-y_2)^2}=\sqrt((0+3)^2+(-3\sqrt3-0)^2)=\sqrt(9+(9 \cdot 3))=\sqrt(9+27)=\sqrt(36)=6[/math]
Quindi, essendo
[math]ar(AB)=ar(AC)=ar(BC)=6[/math]
, il triangolo [math]hat{ABC}[/math]
è equilatero.
Accedi a tutti gli appunti
Tutor AI: studia meglio e in meno tempo
