[math]P[/math]
un punto qualsiasi della base
[math]\bar(AB)[/math]
del triangolo isoscele
[math]hat\{ABC\}[/math]
;
[math]R[/math]
il punto di
[math]\bar(AC)[/math]
tale che
[math]\bar(AR)~=\bar(PB)[/math]
;
[math]S[/math]
punto di
[math]\bar(BC)[/math]
tale che
[math]\bar(SB)~=\bar(AP)[/math]
.Si dimostri che gli angoli
[math]PhatRS[/math]
e
[math]PhatSR[/math]
sono congruenti.
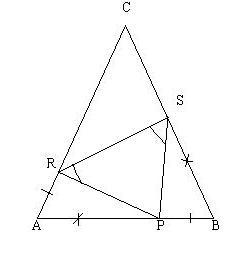
Ipotesi
[math]\bar(AC)~=\bar(CB)[/math]
[math]\bar(AR)~=\bar(PB)[/math]
[math]\bar(SB)~=\bar(AP)[/math]
Tesi
[math]PhatRS~=PhatSR[/math]
.
Dimostrazione
[math]hat\{APR\}~=hat\{BSP\}[/math]
per il primo criterio di congruenza, infatti hanno
[math]\bar(AR)~=\bar(PB)[/math]
per costruzione
[math]\bar(SB)~=\bar(AP)[/math]
per costruzione
[math]PhatAR~=PhatBS[/math]
perchè angoli alla base del triangolo isoscele
[math]hat\{ABC\}[/math]
Di conseguenza risulta anche
[math]\bar(PR)~=\bar(PS)[/math]
e quindi
[math]hat\{PRS\}[/math]
è un triangolo isoscele
e ovviamente risulta che
[math]PhatRS~=PhatSR[/math]
.
Accedi a tutti gli appunti
Tutor AI: studia meglio e in meno tempo
