Sia
[math]ABC[/math]
un triangolo isoscele di base [math]AB[/math]
. Dimostra che la bisettrice dell'angolo esterno di vertice [math]C[/math]
è parallela alla base [math]AB[/math]
.
Risoluzione
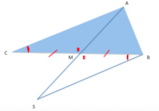
Consideriamo il triangolo isoscele di base[math]AB[/math]
in figura. Chiamiamo con [math]α[/math]
gli angoli congruenti alla base.La bisettrice
[math]b[/math]
divide l'angolo esterno al vertice [math]C[/math]
in due angoli congruenti [math]β[/math]
.Dobbiamo dimostrare che la bisettrice è parallela alla base
[math]AB[/math]
.Sapendo che la somma degli angoli interni di un triangolo è di
[math]180°[/math]
; troviamo quindi l'angolo [math]ACB[/math]
:
[math] hat {ACB} = 180° - 2 \cdot α = 180° - 2α [/math]
Consideriamo ora l'angolo piatto in
[math]C[/math]
, rivolto verso l'interno del triangolo. Esso è formato dai due angoli [math]β[/math]
congruenti generati dalla bisettrice b e dall'angolo interno al triangolo [math]ACB[/math]
, che abbiamo trovato in precedenza e che vale [math]180° - 2α [/math]
.Possiamo quindi trovare il valore di
[math]β[/math]
sottraendo all'angolo piatto l'angolo [math] hat {ACB} [/math]
e dividendo per 2:
[math] β = frac(180° - hat {ACB})(2) = frac(180° - (180° - 2α))(2) = α[/math]
Sappiamo quindi che l'angolo
[math]β[/math]
è uguale all'angolo [math] α[/math]
.
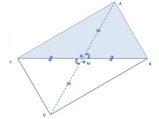
L'angolo in
[math]A[/math]
( [math]α[/math]
bianco) è uguale all'angolo ( [math]α[/math]
nero) generato dalla bisettrice.Per questo motivo, possiamo affermare che sono angoli alterni interni generati da una segmento (
[math]AC[/math]
) tagliato da due trasversali ([math]b[/math]
e [math]AB[/math]
).La bisettrice
[math]b[/math]
e la base [math]AB[/math]
sono quindi paralleli.
Accedi a tutti gli appunti
Tutor AI: studia meglio e in meno tempo
