Rombo: proprietà, caratteristiche ed esercizi svolti

In questo appunto vedremo le proprietà principali del rombo, con le formule utili alla risoluzione dei problemi relativi ad esso. Impareremo inoltre che il rombo è un caso particolare di parallelogramma, ossia un poligono avente quattro lati, a due a due paralleli e congruenti (cioè: i lati non consecutivi sono opposti e congruenti).

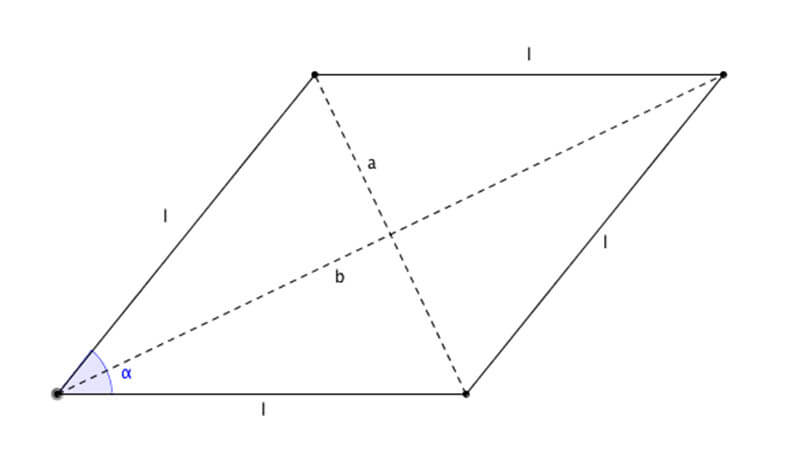
Romboide, parallelogramma e rombo

Se si sta parlando di un romboide o se si sta parlando di un parallelogramma, si sta parlando della stessa figura. Infatti, il romboide è un parallelogramma. Possiamo quindi dire che il rombo è un particolare romboide in cui tutti i lati hanno la stessa misura.
È importante quindi dire che se un certo poligono è un rombo, allora è un romboide, ma se un poligono è un romboide, allora non è detto che esso sia un rombo; infatti i rombi sono un sottoinsieme dei romboidi.
In sintesi: si dice rombo un parallelogramma che ha tutti i lati uguali. Si tratta dunque di un parallelogramma equilatero. Si ricorda che un parallelogramma è un quadrilatero avente i lati opposti paralleli.

Proprietà principali del rombo

Essendo un parallelogramma, esso gode di tutte le proprietà dei parallelogrammi, che sono le seguenti:

• 1) I lati opposti sono uguali (nel caso del rombo TUTTI i lati sono uguali tra loro);


• 2) Ogni diagonale divide il parallelogramma in due triangoli congruenti;


• 3)Gli angoli opposti sono uguali;


• 4) Gli angoli adiacenti a ciascun lato sono supplementari (cioè la loro somma è pari a 180°);


• 5) Le due diagonali si tagliano scambievolmente a metà.

Proprietà caratteristiche del rombo

Oltre alle proprietà sopra citate, il rombo ne ha poi due specifiche:

• 1) Le diagonali sono perpendicolari tra loro. La diagonale più lunga viene detta "diagonale maggiore", mentre quella più corta viene detta "diagonale minore". Le diagonali possono in taluni casi anche essere uguali;


• 2) Le diagonali di un rombo sono bisettrici degli angoli.

Un quadrilatero che non abbia tutte quante queste proprietà non è un rombo, ma un quadrilatero di altro tipo.

Area del rombo

Nel parallelogramma, l'area si trova moltiplicando uno qualsiasi dei suoi lati per l'altezza ad esso relativa. Ebbene, questa caratteristica si ritrova anche nel rombo. Tuttavia, calcolare l'area del rombo attraverso questo metodo risulta molto complesso, perché complesso è il calcolo dell'altezza relativa ad uno qualsiasi dei suoi lati.
Al posto di questo metodo, se ne preferisce dunque un altro. Vediamo quale.

Dopo aver tracciato un rombo, si conducono dai suoi vertici delle rette parallele alle due diagonali (che chiamiamo rispettivamente e ), in modo da formare un rettangolo diviso in otto triangoli. Non è difficile dimostrare che questi otto triangoli sono tutti uguali tra loro.



Il rettangolo ha i lati paralleli alle due diagonali del rombo. Degli otto triangoli che costituiscono l'area di questo rettangolo, il rombo ne contiene solo quattro, cioè la metà. Questo ci porta alla conclusione che l'area del rombo sia pari alla metà dell'area di un rettangolo che ha i lati della stessa misura delle sue diagonali.

Detto più semplicemente: "l'area del rombo si ottiene moltiplicando fra loro le due diagonali e dividendo poi il prodotto per due".



Da questa formula derivano poi due formule inverse, utili per calcolare una delle due diagonali del rombo qualora siano note l'area del rombo e l'altra diagonale.





Per approfondimenti sull'area del rombo vedi anche qua

Esercizio pratico sul rombo

Vediamo insieme un esempio pratico: si tratta di un tipo di esercizio frequentemente richiesto.
"Calcolare il valore delle diagonali di un rombo sapendo che la loro somma è 36 cm ed una è i 4/5 dell'altra".

Chiamiamo e le due diagonali del rombo, rispettivamente quella minore e quella maggiore. Come il problema ci fa sapere:





Come si vede abbiamo due equazioni, che però non siamo in grado di risolvere a causa della presenza di due incognite ( e ).
Sostituiamo allora nella prima equazione il valore di D1 fornitoci dalla seconda. Diviene:




Grazie a questa piccola sostituzione abbiamo trasformato questa equazione in una equazione ad una sola incognita (D2 = x), e che quindi sappiamo ben risolvere utilizzando le nostre conoscenze riguardo alle equazioni di primo grado: sarà sufficiente isolare l'incognita.










Ricordando quanto affermava la seconda equazione, siamo in grado adesso di calcolare anche il valore di .

Il rombo e il teorema di Pitagora

Molto spesso nei problemi di geometria viene assegnato un rombo di cui si conoscono le misure delle due diagonali e , e viene richiesto di calcolarne area (A) e perimetro (2p).

Abbiamo introdotto precedentemente la formula che permette di calcolare l'area del rombo una volta note le sue diagonali. Un pochino più complesso è calcolare il suo perimetro qualora non siano noti i lati, perché richiede stavolta di utilizzare il Teorema di Pitagora.

Sappiamo che nel rombo i quattro lati sono tutti uguali. Dunque, una volta noto il lato (L) del rombo sarà possibile calcolarne il perimetro:




Abbiamo detto precedentemente che le diagonali del rombo sono tra loro perpendicolari e che si tagliano reciprocamente a metà. Stando così le cose, possiamo facilmente dimostrare che esse dividono il rombo in quattro triangoli rettangoli tutti uguali: i due cateti avranno dimensione e , mentre l'ipotenusa sarà il lato del rombo.



Per calcolare il lato (L) del rombo possiamo dunque utilizzare il teorema di Pitagora:






Da questa formula derivano poi due formule inverse, utili per calcolare una delle due diagonali del rombo qualora siano noti il lato del rombo e l'altra diagonale.






Si osservi sempre dalla FIGURA 3 come l'altezza relativa all'ipotenusa di ciascuno dei quattro triangoli in cui il rombo viene diviso dalle sue diagonali sia il raggio della circonferenza inscritta nel rombo, cioè il suo apotema. Tale valore può essere facilmente calcolato nota l'area e il perimetro del rombo, ma se ne risparmia in questa sede la trattazione. Allo stesso modo, conoscerne il valore permette facilmente di calcolarne area e perimetro, con procedimenti diversi da quelli che sono stati descritti in questo appunto. Si rimandano tutte queste questioni agli appunti esplicitamente dedicati all'argomento Apotema.

Per ulteriori approfondimenti sull'apotema vedi anche qua