Distanza tra due punti
Osservazione 1
Comunque consideriamo due punti distinti[math] A(x_A, y_A) [/math]
e [math] B(x_B, y_B) [/math]
di un piano cartesiano risulta definito il segmento ?? avente i due punti come estremi. Esso si può vedere come appartenente alla retta orientata passante per ? e ?, avente ? come origine, ?? come unità di misura e verso crescente da ? a ?.
Vogliamo risolvere il problema di determinare la lunghezza di tale segmento note solo le coordinate dei suoi estremi.
Metodo risolutivo:
Si considerino le perpendicolari agli assi coordinati passanti per ? e ?. Si vede che esse devono necessariamente intersecarsi in un punto ?, il quale in certi casi particolari potrebbe coincidere con uno dei due punti ? e ?; questa eventualità, ad ogni modo, non ci crea alcun problema. Dall'ortogonalità degli assi coordinati segue quella dei segmenti ?? e ??: il triangolo ??? è dunque rettangolo in ?. Per il teorema di Pitagora si avrà allora[math] AB^2 = AC^2 + BC^2 \Rightarrow AB = \sqrt{AC^2 + BC^2} [/math]
pertanto per determinare la lunghezza di ?? non ci resta che conoscere quelle dei segmenti ?? e ??. Osserviamo che il punto ? è allineato verticalmente con ? e orizzontalmente con ?. Allora le distanze sono
[math] AC = | x_B - x_A |,,,, , ,,,, BC = | y_B - y_A | [/math]
I valori assoluti che appaiono nelle formule precedenti sono d'obbligo; infatti la lunghezza di un segmento è sempre positiva, e se per esempio scrivessimo
[math] AC = x_B - x_A [/math]
senza valore assoluto, nel caso possibile in cui [math] x_B \lt x_A [/math]
avremmo [math] AC \lt 0 [/math]
. Ne consegue che la lunghezza di ?? si può calcolare come
[math] AB = \sqrt{AC^2 + BC^2} = \sqrt{|x_B-x_A|^2+|y_B-y_A|^2} \Rightarrow [/math]
[math] AB = \sqrt{(x_B-x_A)^2+(y_B-y_A)^2} [/math]
Questa volta i valori assoluti si possono eliminare: infatti vale che
[math] (x_B - x_A)^2 = (x_A - x_B)^2 [/math]
e ciò significa che possiamo ignorare il segno.
Osservazione 2
Se ? e ? sono allineati verticalmente, cioè hanno la stessa ascissa, ci è già nota una formula ovvia per calcolare la loro distanza:[math] AB = |y_B - y_A| [/math]
. Questa risulta anche come caso particolare da quella appena ottenuta per ? e ? in posizione generica, in quanto da [math] x_A = x_B |[/math]
segue
[math] AB =\sqrt{{x_B-x_A}^2+(y_B-y_A)^2} = \sqrt{0 + (y_B-y_A)^2} = |y_B - y_A| [/math]
Un discorso analogo vale allorché ? e ? sono punti nel piano allineati orizzontalmente.
Osservazione 3
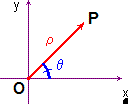
La formula per la distanza tra due punti ci consente, com'è ovvio, anche di trovare la distanza di un punto ? dall'origine. Avendosi in questo caso [/math] x_0 = y_0 = 0[math], sarà
[math] OP = \sqrt{{x_P-x_0}^2+(y_P-y_o)^2} = \sqrt{(x_P-0)^2+(y_p-0)^2} = \sqrt{x^2_P+y^2_P} [/math]
Questa formula tornerà utile durante lo studio della circonferenza nel piano cartesiano.
Segmenti di una retta orientata aventi dato rapporto
Osservazione 4
Siano dati ancora due punti ? e ? e la retta orientata ?? così com'è stata definita nell'osservazione 1. Comunque si prenda un punto ? appartenente al segmento ??, sulla retta orientata ad esso corrisponderà un numero reale ? compreso tra 0 e 1: ciò equivale a dire che[math] (AP)/(AB) = k [/math]
. Il problema che ci proponiamo di risolvere adesso consiste nel trovare le coordinate del punto ? noti il numero ? e le coordinare di ? e ?.
Metodo risolutivo:
Tramite un'applicazione del teorema di Talete, risulta subito chiaro che valgono le proporzioni seguenti:
[math] AP:AB = (y_p-y_A):(y_B-y_A),,,, , ,,,, AP:AB = (x_P-x_A):(x_B-x_A) [/math]
Dal momento che per ipotesi abbiamo che
[math] (AP) / (AB) = k [/math]
le relazioni date si riscrivono come
[math] y_P - y_A = k (y_B - y_A) \Rightarrow y_P = y_A + k (y_B - y_A) [/math]
[math] x_P - x_A = k (x_B - x_A) \Rightarrow x_P = x_A + k (x_B - x_A) [/math]
Per cui le coordinate di ? sono
[math] P(x_A + k (x_B-x_A), y_A + k(y_B-y_A)) [/math]
.
Osservazione 5
La formula ottenuta per le coordinate di ? è capace di fare più di quello per cui è stata scritta. Come sappiamo se sostituiamo a ? un numero compreso tra 0 e 1 otteniamo un punto ? appartenente al segmento ??; in particolare ponendo ?=0 sarà[math] P \sim A [/math]
, mentre con ?=1 sarà [math] P \sim B [/math]
. Se però sostituiamo a ? un numero reale minore di 0 o maggiore di 1, otteniamo altri risultati interessanti: in entrambi i casi avremo che ? appartiene alla retta orientata ??, ma per [math] k \lt 0 [/math]
esso sarà posizionato alla sinistra di ?, mentre per [math] k \gt 1 [/math]
? sarà alla destra di ?.
Punto medio di un segmento
Tra tutti i punti del segmento ?? ce n'è uno notevole: il punto medio ?. Essendo esso l'unico punto tale che ????=12, sostituendo ?=12 nella formula ricavata alla fine del metodo risolutivo otterremo le coordinate di ?:
[math] M \Big(x_A + \frac{1}{2}(x_B-x_A), y_A + \frac{1}{2}(y_B-y_A) \Big) \Rightarrow M \Big( \frac{x_A+x_B}{2}, \frac{y_A+y_B}{2} \Big) [/math]
Si vede così che le coordinate del punto medio di un segmento ?? coincidono con la media aritmetica delle coordinate degli estremi del segmento.
Il baricentro di un triangolo
Ricordiamo dalla geometria classica che il \baricentro di un triangolo ??? è definito come punto d'incontro delle sue mediae, ovvero delle rette che congiungono ciascun vertice del triangolo con il punto medio del lato opposto. Per trovare le coordinate del baricentro ? di un triangolo qualsiasi utilizzeremo un'altra sua proprietà: il baricentro di un triangolo divide ciascuna delle sue mediane in due segmenti le cui lunghezze stanno tra loro come 1 sta a 2. Stando alla figura che segue, siamo alla ricerca di un punto ? tale che ??=2 ??, o il che è lo stesso
[math] \frac{CG}{CM} = \frac{2}{3} [/math]
.Per trovare ? adoperiamo ancora la stessa formula dell'esempio precedente, ma stavolta
[math] k = \frac{2}{3} [/math]
e gli estremi del segmento sono ? ed ?:
[math] G \Big(x_C+\frac{2}{3}(x_M-x_C) , y_C + \frac{2}{3}(y_M-y_C) \Big) \Rightarrow G \Big( \frac{2}{3}x_M+\frac{x_C}{3}, \frac{2}{3} y_M + \frac{y_C}{3} \Big) [/math]
Non ci resta che sostituire a
[math] x_M [/math]
e [math] y_M [/math]
le coordinate del punto medio di ?? trovate nell' esempio 1 per ottenere la soluzione:
[math] G \Big( \frac{2}{3} \cdot \Big(\frac{x_A+x_B}{2}\Big) + \frac{x_C}{3}, \frac{2}{3} \cdot \Big(\frac{y_A+y_B}{2} \Big) + \frac{y_C}{3} \Big) \Rightarrow [/math]
[math] G \Big( \frac{x_A+x_B+x_C}{3}, \frac{y_A+y_B+y_C}{3} \Big) [/math]
Accedi a tutti gli appunti
Tutor AI: studia meglio e in meno tempo
