Fascio di circonferenze

Elementi di un fascio di circonferenzeDefinizione 1:

Definizione di fascio di circonferenze

Si considerino due circonferenze non concentriche ( Gamma_1 ) e ( Gamma_2 ) di equazioni rispettivamente ( x^2+y^2+alpha_1x+\beta_1x+gamma_1 = 0 ) e ( x^2+y^2+alpha_2x+\beta_2x+gamma_2 = 0 ). Si chiama fascio di circonferenze di prima generatrice ( Gamma_1 ) e seconda generatrice ( Gamma_2 ) la combinazione lineare

[ \begin{equation} Phi: x^2+y^2+alpha_1x+\beta_1y+gamma_1+\ +k(x^2+y^2+alpha_2x+\beta_2y+gamma_2) = 0 label{eq1} end{equation} ]

con ? parametro reale.

Osservazione 1: Se nell'equazione ((\ref{eq1})) del fascio svolgiamo i calcoli e mettiamo in evidenza possiamo ottenere, qualora sia ( k
e -1 ),

[ \begin{equation} Phi: x^2+y^2+Big( frac{alpha_1+kalpha_2}{k+1} Big)x+Big( frac{\beta_1+k\beta_2}{k+1} Big)y+ \ + Big( frac{gamma_1+kgamma_2}{k+1} Big) = 0 label{eq2} end{equation} ]

Questa maniera di scrivere l'equazione del fascio ( Phi ) sottolinea come, al variare di ( k in mathbb{R}, k
e -1 ), esso descriva una famiglia infinita di circonferenze, la cui equazione canonica è appunto la ((\ref{eq2})).

Osservazione 2: Se nell'equazione ((\ref{eq1})) del fascio si sostituisce ?=0, quella che si ottiene è una circonferenza particolare, la prima generatrice (Gamma_1).

Non esiste invece valore di ? tale da far ottenere la seconda generatrice (Gamma_2): in verità si dice, anche se a questo punto del corso di studi non si è nelle condizioni di capire bene il perché, che (Gamma_2) si ottiene per ( k = infty ). Ad ogni buon conto i ruoli delle due generatrici non sono simmetrici, il che giustifica i nomi con cui vengono distinte.

Definizione 2: Definizione di asse radicale

Si definisce asse radicale di un fascio di circonferenze ( Phi ) la retta che si ottiene sostituendo nella sua equazione il valore ?=−1. L'equazione dell'asse radicale ? è dunque

[ \begin{equation} r: (alpha_1-alpha_2)x+(\beta_1-\beta_2)y+(gamma_1-gamma_2) = 0 label{eq3} end{equation} ]

Osservazione 3: Anche l'asse radicale ?, che è una retta, si può considerare una particolare circonferenza: esso può infatti essere visto come una circonferenza degenere di raggio infinito. Si può notare infatti che, se nell'equazione ((\ref{eq2})) sostituiamo valori di ? sempre più vicini a 1, i raggi delle circonferenze propriamente dette ottenute sono via via più grandi. Questa osservazione ci consente di dire che tutte le curve descritte dal fascio ( Phi ) sono, in qualche modo, delle circonferenze.

Osservazione 4: Proviamo a prendere due qualsiasi circonferenze di ( Phi ) e a intersecarle. Otterremo così, fissati due parametri reali ? e â„Ž distinti da −1 e diversi tra loro, il sistema

[ \begin{cases}Gamma_K \ Gamma_H end{cases} Rightarrow \begin{cases} x^2+y^2+Big(frac{alpha_1+kalpha_2}{k+1}Big)x+Big(frac{\beta_1+k\beta_2}{k+1}Big)y+Big(frac{gamma_1+kgamma_2}{k+1}Big) = 0 \ x^2+y^2+Big(frac{alpha_1+halpha_2}{h+1}Big)x+Big(frac{\beta_1+h\beta_2}{h+1}Big)y+Big(frac{gamma_1+hgamma_2}{h+1}Big) = 0 end{cases} ]

Sottraendo la seconda equazione dalla prima, otteniamo che una delle equazioni a nostra scelta può essere sostituita dalla più semplice

[ Big(frac{alpha_1+kalpha_2}{k+1}-frac{alpha_1+halpha_2}{h+1}Big)x + Big(frac{\beta_1+k\beta_2}{k+1}-frac{\beta_1+h\beta_2}{h+1}Big)y + Big(frac{gamma_1+kgamma_2}{k+1}-frac{gamma_1+hgamma_2}{h+1}Big) = 0 ]

la quale, svolgendo i conti in parentesi, si riduce infine alla

[ (alpha_1-alpha_2)x+(\beta_1-\beta_2)y+(gamma_1-gamma_2) = 0 ]

che è proprio l'equazione ((\ref{eq3})) dell'asse radicale. Si noti anche che l'equazione ottenuta non dipende da nessuno dei due parametri â„Ž e ?. Quindi abbiamo scoperto queste equivalenze tra sistemi:

[ \begin{equation}\begin{cases} r \ Gamma_H end{cases} Leftrightarrow \begin{cases} Gamma_K \ Gamma_H end{cases} Leftrightarrow \begin{cases} Gamma_K \ r end{cases}label{eq4} end{equation} ]

La prima equivalenza ci dice che le intersezioni tra ( Gamma_K ) e ( Gamma_H ) non dipendono da ?, la seconda che esse non dipendono neanche da â„Ž; ne deduciamo che tutte le circonferenze del fascio si intersecano negli stessi punti, che in virtù delle equivalenze ((\ref{eq4})) appartengono anche all'asse radicale.

Definizione 3: Definizione di punti base

Si chiamano punti base di un fascio di circonferenze ( Gamma ) i punti d'intersezione comuni a tutte le circonferenze del fascio. Essi possono essere in numero di 0, 1 o 2.

Osservazione 5: In virtù dell'osservazione 4, la definizione di punti base è lecita, in quanto tutte le circonferenze del fascio si intersecano negli stessi punti. Poiché tali punti si possono trovare anche intersecando l'asse radicale con una qualsiasi delle circonferenze del fascio, i punti base non possono essere più di 2. Essi saranno 0, 1 o 2 a seconda che le generatrici ( Gamma_1 ) e ( Gamma_2 ) siano disgiunte, tangenti o secanti.

Osservazione 6: Dall'equazione del fascio ((\ref{eq2})) possiamo ricavare le coordinate del centro di una generica circonferenza appartenente al fascio. Esse saranno, come sappiamo,

[ CBig(-frac{alpha}{2},-frac{\beta}{2} Big) Rightarrow CBig( -Big(frac{alpha_1+kalpha_2}{2k+2}Big), -Big( frac{\beta_1+k\beta_2}{2k+2} Big) Big) ]

ovvero ( x = -Big( frac{alpha_1+kalpha_2}{2k+2} Big), y = - Big( frac{\beta_1+k\beta_2}{2k+2} Big) ). Se risolviamo la prima delle due equazioni per ? e sostituiamo il valore ottenuto nella seconda avremo, dopo qualche calcolo,

[ \begin{equation} k=-frac{2x+alpha_1}{2x+alpha_2} Rightarrow (\beta_1-\beta_2)x-(alpha_1-alpha_2)y+frac{\beta_1alpha_2-\beta_2alpha_1}{2} = 0 label{eq5} end{equation} ]

Cosicché, indipendentemente da quale sia il valore di ?, le coordinate del centro della circonferenza del fascio ad esso relativa soddisfano l'equazione ottenuta alla fine del conto precedente, che è quella di una retta. Ciò prova che i centri di tutte le circonferenze del fascio appartengono a una stessa retta.

Definizione 4: Definizione di retta dei centri

Si chiama retta dei centri di un fascio ( Phi ) la retta cui appartengono i centri di tutte le circonferenze del fascio.

Osservazione 7: La retta dei centri di un fascio di circonferenze è sempre perpendicolare al suo asse radicale. Se infatti calcoliamo i coefficienti angolari delle rette le cui equazioni sono ((\ref{eq3})) e ((\ref{eq5})), abbiamo

[ m_1 = -Big( frac{alpha_1-alpha_2}{\beta_1-\beta_2} Big),,,,,,, m_2 = frac{\beta_1-\beta_2}{alpha_1-alpha_2} Rightarrow m_1m_2 = -1 ]

che è giustappunto la condizione di ortogonalità tra due rette. Inoltre, già sappiamo dalla geometria elementare che se due circonferenze i cui centri giacciono su una stessa retta si intersecano in due punti, questi sono simmetrici rispetto alla retta dei centri. Questo fatto, unitamente alla relazione di perpendicolarità appena dimostrata e alle osservazioni precedenti, prova che la retta dei centri è l'asse del segmento i cui estremi sono i punti base. Nella condizione limite in cui il punto base è uno solo, questo sarà naturalmente il punto d'intersezione tra la retta dei centri e l'asse radicale.

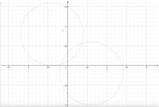
Osservazione 8: Tutte le osservazioni 1 - 7 e le definizioni 1 - 4 sono rappresentate nelle due seguenti immagini; la prima di esse mostra la situazione con due punti base ? e ?,

la seconda invece quella con un solo punto base ?.

L'asse radicale è sempre rappresentato in rosso, mentre la retta dei centri appare in blu. Le due circonferenze generatrici del fascio sono tracciate in nero, e la terza rappresentata in grigio tratteggiato è una circonferenza qualsiasi appartenente al fascio. Si noti in particolare come, nel secondo caso, l'asse radicale sia tangente a tutte le circonferenze del fascio nel punto base ?.