Nuove direttive post riordino: Innovazione nella didattica della matematica e stili di apprendimento induttivi

Il servizio scolastico

Il servizio scolastico camba, formulando nuove direttive per l’innovazione della didattica: “uso costante del laboratorio nell’insegnamento delle discipline scientifiche”; “metodologie finalizzate a valorizzare il metodo scientifico e il pensiero operativo”; "valorizzare stili di apprendimento induttivi". Questo scritto ha un duplice obiettivo: da un lato vuole attribuire un univoco significato alle parole chiave della norma fondante l’autonomia scolastica, terreno su cui radicherà il nuovo modello di scuola, dall’altro lato fornire un esempio di didattica laboratoriale. In particolare si presentano e si discutono tre questioni.
Il servizio scolastico camba: i nuovi regolamenti approvati dal C.d.M. il 4/2/10 formulano direttive per l’innovazione della didattica. Tra queste: “L’uso costante del laboratorio nell’insegnamento delle discipline scientifiche” [licei]; “metodologie finalizzate a valorizzare il metodo scientifico e il pensiero operativo”; [ist. tecnici]; valorizzare stili di apprendimento induttivi [ist. professionali], norme che implicano il superamento dell’insegnamento cattedratico.
Questo aspetto non esaurisce la riorganizzazione in atto in quanto questa si qualifica soprattutto per la ristrutturazione della scuola: i profili di fine quinquennio, che elencano le competenze generali che gli studenti dovranno esibire, presuppongono l’unitarietà di tutti gli insegnamenti, vale a dire il superamento della loro parcellizzazione. Si valuti, ad esempio, l’impatto sull’organizzazione scolastica dei traguardi: “Consapevolezza della diversità dei metodi utilizzati dai vari ambiti disciplinari e valutazione dei criteri di affidabilità dei risultati in essi raggiunti” [licei] oppure “utilizzo degli strumenti culturali e metodologici acquisiti per porsi con atteggiamento razionale, critico e responsabile di fronte alla realtà, ai suoi fenomeni e ai suoi problemi” [ist. Tecnici].
Questo scritto ha un duplice obiettivo: da un lato vuole attribuire un univoco significato alle parole chiave della norma fondante l’autonomia scolastica, terreno su cui radicherà il nuovo modello di scuola, dall’altro lato fornire un esempio di didattica laboratoriale.

Prima questione

Avete trascorso dai nonni in Toscana le vostre vacanze estive. Il nonno una sera ha chiesto consiglio a tutta la famiglia riunita a tavola a proposito di un suo progetto: coltivare a frutteto tutta l’ampia zona circostante la sua abitazione. Aveva comperato 5.000 piante di melo di un anno (astoni) e voleva ottenere alberi di forma equilibrata e di buona produttività, fruttificazione favorita dalla luce, dall’areazione e dalla distanza tra le mele. Bisognava predisporre un adeguato piano di potatura: da ogni gemma, l’anno successivo, si svilupperà un ramo identico all’astone.
Per esempio: se un astone oggi presenta dieci gemme, ne presenterà cento il successivo, mille tra due anni. Quale consiglio avreste dovuto dare al nonno?

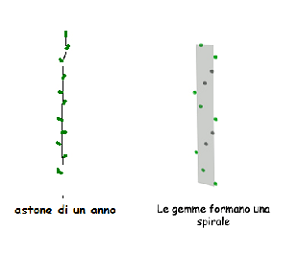
Seconda questione

Leonardo da Pisa è figura di rilievo nello scenario scientifico italiano. Classico il suo studio del seguente problema: si supponga che
• In una gabbia ci sia chiusa una coppia di conigli adulti (un maschio e una femmina);
• Ogni mese una coppia adulta genera una nuova coppia (maschio e femmina) di conigli;
• Che i nuovi nati giungano a maturità (capacità di generare) all’età di un mese(al secondo mese di vita diventano genitori, nascono i coniglietti);
• Nessun coniglio muoia. Quanti conigli ci saranno alla fine di un anno?

Terza questione

Un vostro vicino di casa, che frequenta la quinta classe della scuola primaria, non riuscendo a risolvere un problema di matematica, vi chiede aiuto. Il testo del problema è il seguente: “Un venditore di caldarroste, durante il mese di gennaio ha comperato 20 chilogrammi di castane a € 2 al chilogrammo e ancora 25 chilogrammi a € 2,20. Ha rivenduto le castagne a € 1,50 il pacchetto da 200 grammi, riuscendo a vendere tutte le castagne acquistate. Sapendo che per la caldaia ha comperato 1,30 quintali di carbone a € 0,10 il chilogrammo e che non ne ha consumato 15 chilogrammi, si determini il guadagno conseguito.” Individuate un procedimento esplicativo che faciliti la comprensione di questa classe di problemi.