Motoscafo

Georges Dupont è un bancario che vive in un villaggio della costa francese sulla Manica. È uno scapolo con molti hobby. In particolare possiede un motoscafo che utilizza il fine settimana per spostarsi velocemente lungo la costa. Di recente ha conosciuto Jane
una ragazza inglese che abita sul lato britannico del Canale. Che per gli inglesi è The English Channel, mentre per i francesi è La Manche. Per fare colpo Georges decide di andare a farle visita con il motoscafo: finora non ha mai attraversato il canale, ma pensa che non ci saranno difficoltà.

Schematizziamo il problema come riportato nella figura sotto.

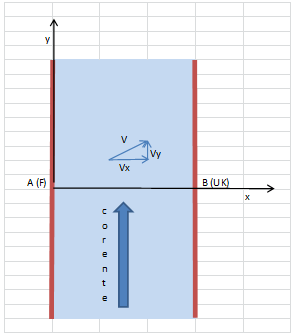
Georges progetta di attraversare la Manica andando da A(Francia) a B(UK) con rotta lungo l'asse x. La distanza AB è di 40 km e George la percorrerà a velocità costante

. Il tempo della traversata sarà dunque di 40/25 = 1,6 h, che vuol dire 96 minuti. Disponendo di una carta nautica e della bussola Georges parte.

Tuttavia la traversata si rivela un po' diversa da come pianificato. Georges ha ignorato/sottovalutato l'esistenza di una corrente che lo farà deviare dalla rotta. La corrente, causata dal flusso di marea, è diretta secondo l'asse y e può raggiungere una velocita media di 5 - 10 km/h. Desideriamo prevedere dove andrà a finire Georges.

Cominciamo a notare che il motoscafo si muove lungo l'asse x alla velocità

ed inoltre è soggetto alla velocità di trascinamento causata dalla corrente. La risultante delle due velocità, come ci insegna la Cinematica, è V, la somma vettoriale di e , come si vede in figura. Ora se fosse costante anche V sarebbe costante e quindi il motoscafo si muoverebbe in diagonale lungo un linea retta. Nella realtà la faccenda è più complicata perché la corrente è variabile da punto a punto e imprevedibile: ciò è dovuto alla sua natura turbolenta. Immaginiamo di rappresentare la velocità con una semplice funzione:

[ \begin{equation} V_y = V_{\text{ymax}} Big[ 1- frac{4}{h^2}Big( x-frac{h}{2} Big)^2Big] + k cdot \text{Casuale()} ,,,, \text{per } 0 lt x lt h label{eq1}end{equation} ]

mentre

[ V_y = 0 ,,,, \text{ per } x = 0 \text{ ed } x = h ]

Dove h è la larghezza del Canale, e quindi la distanza AB. La ((\ref{eq1})) è la somma di due termini. Il primo è una funzione parabolica della x, che si azzera per x=0 ed x=h (

è nulla sulla riva) e massima per .

Il secondo è una variabile casuale a distribuzione uniforme con

[ \text{Media} = frac{k}{2} ,,,,,, \text{Deviazione Standard} = \sqrt{frac{k}{12}} ]

ottenibile con la funzione matematica casuale() di EXCEL moltiplicata per la costante k.

Supponiamo che sia (V_{\text{ymax}} = 5km/h ) e (k = 5\text{km}/h) La funzione ((\ref{eq1})) si calcola con EXCEL ed il suo diagramma (profilo di velocità), ad esempio, potrebbe essere il seguente:

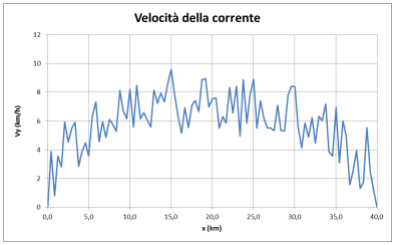
Il file EXCEL allegato a questo articolo riporta i semplici calcoli nello Sheet VELOCITA'

. Posizionandosi nello Sheet e premendo F9 viene ricalcolato l'intero profilo di velocità. Possiamo immaginare che il profilo sopra riportato rappresenti l'andamento effettivo di in una traversata. Supponiamo anche che a ogni nuova traversata (in andata) corrisponda un diverso profilo di velocità.

Il passo successivo che dobbiamo fare è il calcolo della rotta del motoscafo, vale a dire determinare (x=f(t)) ed (y=g(t)) e di conseguenza y in funzione di x. Sappiamo che, per definizione, la velocità è la derivata dello spazio (percorso) rispetto al tempo. E questo può essere scritto, separatamente, per le due direzioni x ed y:

[ \begin{equation} frac{dx}{dt} = V_x label{eq2} end{equation} ]

[ \begin{equation} frac{dy}{dt} = V_y label{eq3} end{equation} ]

Le due equazioni differenziali ((\ref{eq2})) e ((\ref{eq3})) devono soddisfare rispettivamente le condizioni iniziali: [ t=0,,,, x=0,,,, y=0 ]

Ora notiamo che, avendo assunto

costante, si ottiene immediatamente la soluzione della ((\ref{eq2})):

[ \begin{equation} x=int_0^t V_x, dt = V_xt label{eq4} end{equation} ]

Integrazione della ((\ref{eq3})) è meno semplice essendo

una funzione di x e dei valori casuali.

Volendo tracciare, punto per punto, la rotta è necessario integrare la ((\ref{eq3})) con un procedimento numerico. Proponiamo l'uso del Metodo di Eulero: si sostituiscono i differenziali con (piccoli) incrementi finiti. La ((\ref{eq3})) diventa: [ Delta y = V_y Delta t ]

Che scritta in forma più conveniente diventa:

[ \begin{equation} y_{n+1} = y_n + V_{y,n} Delta t label{eq5} end{equation} ]

Basta scegliere un passo di integrazione, ad es. ( Delta t = 1 \text{minuto} ) e calcolare passo- passo,

con la ((\ref{eq1})) ed i valori di y con la ((\ref{eq5})).

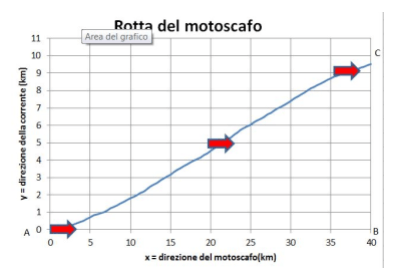
Un calcolo tipico è riportato nello Sheet Rotta Traversata. Il nostro amico Georges raggiungerà la costa britannica non nel punto B desiderato, ma in un punto C, lungo la corrente, a distanza (Y_{\text{finale}}) da B. Dove (Y_{\text{finale}} =Y(x=40)).

Qui sotto vediamo l'esempio della rotta calcolata. Dove risulta (Y_{\text{finale}} = 9.5 km ).

Notiamo per inciso che durante tutta la traversata l'asse del motoscafo (rappresentato dalla freccia rossa) è sempre orientato in direzione x, tuttavia la rotta è una diagonale nell' asse x,y.

Ora, premendo di nuovo F9 nello Sheet citato, si può calcolare la rotta di una nuova traversata. In tal modo si vede che a ogni nuova traversata (vale a dire nuovo ricalcolo F9) si giunge, sulla costa britannica, a una diversa distanza (Y_{\text{finale}}). Come era facilmente intuibile, in presenza di variabili casuali il risultato finale è pure una variabile casuale.

Con riferimento allo Sheet menzionato, notiamo che avendo deciso di effettuare una integrazione piuttosto precisa abbiamo preso un passo molto piccolo (1 minuto). In questo modo l'integrazione ha richiesto 96 passi. Ciò ha reso necessaria la valutazione di

, e quindi della funzione casuale(), 95 volte. In definitiva il nostro semplice modello matematico contiene 95 variabili casuali indipendenti. Ognuna di queste è definita nell'intervallo 0-1 e ha una funzione di distribuzione uniforme. Ovviamente la distanza BC, che è l'output (risultato) del modello, è a sua volta una variabile casuale.

Dobbiamo concludere che per una specifica traversata non è possibile prevedere con esattezza dove sarà il punto C di arrivo.

Tuttavia la Statistica è stata inventata proprio per aiutarci a calcolare dove, in media, sarà il punto C se ripercorriamo la traversata un numero n abbastanza grande di volte. Se n è molto grande è intuitivo - ma non sicuro a priori - presumere che la distanza BC raggiunga una posizione di equilibrio, tale che aumentando n, il valore BC cambi di una quantità trascurabile. Un calcolo di questo genere si chiama Metodo di Montecarlo. Un ampia descrizione del quale si trova in un recente articolo di Roberto Chiappi in questo website (vedere Bibliografia).

Ora lo Sheet Rotta Traversata va bene per calcolare la posizione finale per qualche iterazione. Ma l'esperienza insegna che per raggiungere l'equilibrio- se l'equilibrio esiste - è necessario almeno qualche migliaia o decina di migliaia di iterazioni. Cosa non fattibile - o quantomeno molto scomoda- con uno Sheet EXCEL.

Il modello matematico che vogliamo scrivere ora, tramite un semplice codice, ha il solo scopo di determinare la distanza finale BC, trascurando il calcolo punto-punto della rotta.

Riprendiamo allora la ((\ref{eq3})) e integriamola.

Si ottiene:

[ y = int_0^t V_y, dt = int_0^t Big{ V_{\text{ymax}} Big[1 -frac{4}{h^2}Big(x-frac{h}{2}Big)^2Big] + k cdot \text{Casuale()}_i Big}, dt ]

E ricordando che x(t) è ormai disponibile dalla ((\ref{eq4})):

[ \begin{equation} y=int_0^t V_y, dt=int_0^t Big{ V_{\text{ymax}}Big[1-frac{4}{h^2}Big(V_xt-frac{h}{2}Big)^2Big]+k\text{Casuale()}_i Big}, dt label{eq6} end{equation} ]

Ora integriamo la ((\ref{eq6})) rispetto al tempo, ricordandoci inoltre di sommare le 95 variabili casuali:

[ \begin{equation} y approx frac{2V_xV_{\text{ymax}}t^2}{3h^2}(3h-2V_xt)+kDelta t\sum_{i=1}^{95} \text{Casuale()}_i label{eq7}end{equation} ]

Notiamo che nella ((\ref{eq7})) l'integrazione della parte casuale è stata ottenuta in modo numerico (e quindi approssimato). Sostituendo nella ((\ref{eq7})) i valori

( durata della traversata, in ore) e (Delta t = frac{1}{60} ) ( passo di integrazione) si ottiene la distanza (BC = y_{\text{finale}}).

Entriamo nello Sheet Dati e risultati per codice VBA. Nell'area gialla sono riportati i dati del problema.

Se ora apriamo la finestra EXCEL Visual Basic con ALT F11 possiamo leggere il semplice codice.

Posizionando il cursore all'inizio delle istruzioni ed eseguendo il codice (con F5) si ottiene (dopo alcuni minuti…) il risultato per (Y_{\text{finale}}) e risulta: media = 9.29 km, deviazione standard = 0.24 km

L'andamento della convergenza (in questo esempio dopo 30 mila iterazioni) è riportato nel diagramma sotto:

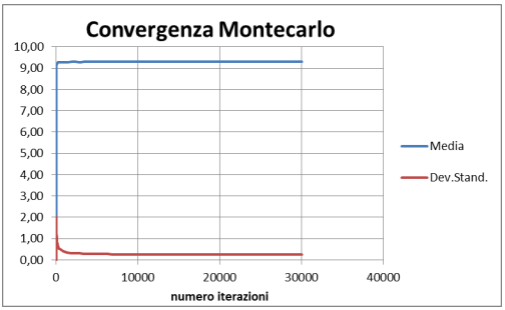
Notiamo che la media converge velocemente, mentre la deviazione standard richiede molti più passi.

Il diagramma seguente evidenzia l'istogramma della funzione Densità di Distribuzione della variabile (Y_{\text{finale}})

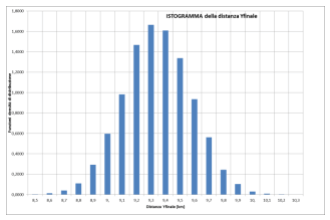
E' quindi una funzione a campana che, grosso modo, somiglia alla distribuzione normale. Questo non dovrebbe essere motivo di sorpresa, in quanto il Teorema Centrale della Statistica ci assicura che, sommando tra loro un numero abbastanza elevato (in pratica > 30) di variabili casuali di qualsiasi tipo, si ottiene una distribuzione prossima alla normale.

Conclusione

Se il nostro amico Georges, dopo il travagliato viaggio, è stato ben accolto da Jane e dunque medita di farle nuove visite in motoscafo, farà bene a studiare un po' di Cinematica e a procurarsi un GPS.

Appendice Distribuzioni

Di seguito riportiamo una breve descrizione dei due tipi di distribuzione citati dall'articolo.

Distribuzione Uniforme - corrispondente alla funzione EXCEL casuale()

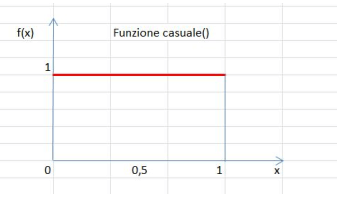
Dove in ascissa abbiamo i valori della variabile casuale x, definita nell'intervallo 0…”1 , mentre in ordinata è la sua funzione densità di distribuzione f(x). L'area sotto la funzione, compresa tra due valori

e qualsiasi, rappresenta la probabilità che la variabile casuale x cada in tale intervallo. E quindi l'area tra 0 e 1 è unitaria (probabilità 100%). Notiamo che f(x) è costante, ed è per questo che si chiama distribuzione uniforme. Che cosa significa? Che nell'intervallo assegnato qualunque valore di x ha la medesima densità di probabilità.

La media della variabile x è data, per definizione, da

( mu = int_0^1 x cdot f(x), dx = int_0^1 x cdot 1, dx = frac{1}{2} )

La varianza e data da:

( int_0^1(x-mu)^2cdot f(x), dx = int_0^1 Big(x-frac{1}{2}Big)^2 cdot 1 cdot dx = )

( frac{1}{3}Big[Big(1-frac{1}{2}Big)^3-Big(-frac{1}{2}Big)^3Big]=frac{1}{12} )

E quindi la deviazione standard è ( \sigma = frac{1}{\sqrt{12}} )

Distribuzione Normale: è ben nota e importante la curva la cui densità di distribuzione è data dall'equazione:

[ f(x) = frac{1}{\sigma\sqrt{2pi}} expBig[-frac{1}{2}frac{(x-mu)^2}{\sigma^2}Big] ]

Ed è definite nell'intervallo (] -infty; +infty [)

Riferimenti

• https://www.skuola.net/approfondimenti/problem-solving/introduzione-al-metodo-montecarlo/
• Mohammed A. Shayib - Applied Statistics - ISBN 978-87-403-0493-0
• Darius Singpurwalla - A handbook of Statistics - ISBN 978-87-403-0545-5
• David Brink - Essential of Statistics-Exercises - ISBN 978-87-7681-409-0
• https://en.m.wikipedia.org/wiki/Central_limit_theorem