Analisi - Teoremi sulle funzioni derivabili

: data una funzione y = f(x) continua nell’intervallo chiuso e limitato [a; b] e derivabile(*) nell’intervallo aperto (a; b) esiste almeno un punto c, interno all’intervallo [a; b] tale che risulti:

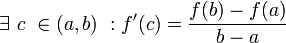
(*)La definizione è valida nel momento in cui una funzione presenta in un punto x0 derivata finita. Pertanto la derivata di una funzione f(x) in un punto x0 è il limite, se esiste, del rapporto incrementale, al tendere a zero dell’incremento dato alla variabile indipendente. Data la definizione si ha dunque:

Teorema di Rolle : data una funzione y = f(x) continua nell’intervallo chiuso e limitato [a; b] e derivabile nell’intervallo aperto (a; b),e assume valori uguali f(a) = f(b), esiste almeno un punto c, interno all'intervallo aperto (a,b) per cui la derivata si annulla, ossia:

teorema di cauchy:date due funzioni f(x) e g(x), continue nell'intervallo chiuso [a,b], derivabili nei punti interni dell'intervallo aperto (a,b) e sia la derivata di g(x) diversa da zero per ogni punto dell'intervallo, allora esiste almeno un punto c interno all'intervallo chiuso [a,b] per il quale si ha:

caso particolare: ponendo g(x) = x, otteniamo il teorema di Lagrange

teorema di de l'hopital: date due funzioni f(x) e g(x) definite in un intorno di c, escluso al più c stesso, e tali che il limite di f(x) per x che tende a c sia uguale al limite di g(x) per x che tende a c. Inoltre se le due funzioni sono derivabili nell'intorno di c, escluso al più c stesso, e la derivata prima di g è diversa da zero, e se esiste il limite per x che tende a c del rapporto delle derivate prime di fx e gx, allora esisterà anche il limite per x che tende a c, delle due funzioni, e il valore di tali limiti, sarà uguale.