Primo Teorema Fondamentale del Calcolo
Sia f una funzione continua in un intervallo aperto contenente l'intervallo [a, b].
Sia 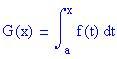
.
Secondo Teorema Fondamentale del Calcolo
Se f è continua in [a, b] e se F è una qualunque primitiva di f, allora:
I due teoremi ci dicono che:
1) Ogni funzione continua ha una primitiva;
2) Per valutare l'integrale definito di una funzione continua, trova una sua primitiva e valutala negli estremi dell'intervallo.
Quello che i Teoremi Fondamentali del Calcolo non garantiscono è che la primitiva di una funzione continua possa essere scritta in termini di funzioni elementari: polinomi, seno, coseno, radici, esponenziali e logaritmi. Essi ci danno, comunque, un semplice metodo per valutare l'integrale permettendoci di scegliere una qualsiasi primitiva della funzione integranda.
Trova
Una primitiva di è
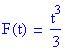
In una sezione precedente, abbiamo valutato questo integrale usando le somme di Riemann e prendendo il limite per la norma della partizione tendente a zero.
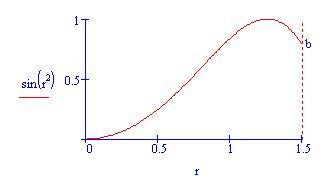
Trova l'area tra l'asse x e la curva sin(x 2 ) tra x = 0 e x = 1.5.
Estremi dell'intervallo:
L'area è il valore dell'integrale
Cerchiamo di trovare la primitiva di sin(x 2) .
per integrazione, si ha
Cos'è questa funzione FresnelS? E' un modo mascherato di scrivere l'integrale di sin(x 2 ).
Questo significa che non esiste un'espressione dell'integrale di sin(x 2 ) in termini di funzioni elementari. Il massimo che possiamo fare è calcolare l'integrale numericamente.
Consideriamo lo sviluppo in serie della funzione
Sviluppiamo in serie questa funzione arrestandoci al 20-simo termine
Integrando termine a termine si avrà:
Ovviamente maggiore è l'ordine dello sviluppo in serie della funzione più accurato è il valore dell'area calcolata numericamente!

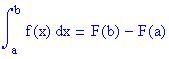
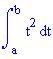
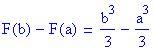
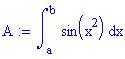
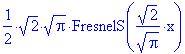
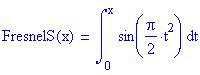
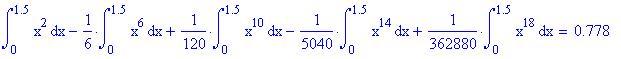





 Accedi a tutti gli appunti
Accedi a tutti gli appunti
 Tutor AI: studia meglio e in meno tempo
Tutor AI: studia meglio e in meno tempo