Teorema fondamentale del calcolo integrale
Sia
[math]f[/math]
una funzione reale continua in un intervallo [math][a,b][/math]
chiuso e limitato.Allora la funzione integrale
[math]F[/math]
, definita come segue, è derivabile nell’intervallo [math][a,b][/math]
e risulta [math]F’(x) = f(x)[/math]
per ogni valore [math]x \in [a,b][/math]
.
[math]F(x) = \int_{a}^{x} f(t) dt[/math]
Dimostrazione
Si considera il rapporto incrementale della funzione integrale
[math]F[/math]
in base alla sua definizione, applicando la proprietà di linearità dell’integrale:
[math]\frac{F(x + h) – F(x)}{h} = \frac{1}{h} [\int_{a}^{x + h} f(t) dt - \int_{a}^{x} f(t) dt] =\\
=\frac{1}{h} [\int_{a}^{x} f(t) dt + \int_{x}^{x+h} f(t) dt - \int_{a}^{x} f(t) dt] = \frac{1}{h} \int_{x}^{x+h} f(t) dt[/math]
=\frac{1}{h} [\int_{a}^{x} f(t) dt + \int_{x}^{x+h} f(t) dt - \int_{a}^{x} f(t) dt] = \frac{1}{h} \int_{x}^{x+h} f(t) dt[/math]
Stando al teorema del valore medio integrale, deve esistere nell’intervallo
[math][x, x+h][/math]
un punto [math]x_h[/math]
, dipendente dal valore di [math]h[/math]
, tale che:
[math]f(x_h) = \frac{1}{h} \int_{x}^{x+h} f(t) dt = \frac{F(x+h) – F(x)}{h}[/math]
E se
[math]h \rightarrow 0[/math]
, [math]x_h \rightarrow x[/math]
, essendo [math]x \le x_h \le x + h[/math]
.Perciò, ricordando che la funzione
[math]f[/math]
è continua:
[math]\lim_{h \to 0} f(x_h) = f(x)[/math]
Si può concludere che:
[math]F’(x) = \lim_{h \to 0} \frac{F(x+h) – F(x)}{h} = \lim_{h \to 0} f(x_h) = f(x)[/math]
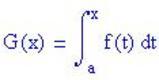
Accedi a tutti gli appunti
Tutor AI: studia meglio e in meno tempo
