Valore assoluto
Definizione
Il valore assoluto è una funzione reale di variabile reale,
[math]|\cdot|: \mathbb{R} \to \mathbb{R}[/math]
, che associa alla variabile [math]x[/math]
il numero stesso se [math]x[/math]
è non negativa, [math]-x[/math]
se invece [math]x[/math]
è negativa. Il valore assoluto di [math]x[/math]
si indica con [math]|x|[/math]
, e risulta
[math]|x| = \begin{cases} x & \quad \text{se } x \ge 0 \\ -x & \quad \text{se } x > 0 \ \end{cases}[/math]
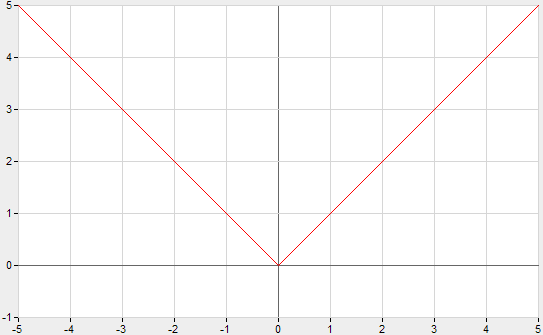
Di seguito viene riportato il grafico della funzione valore assoluto.
Proprietà del valore assoluto
Il valore assoluto è una funzione definita positiva, in quanto gode delle due seguenti proprietà
[math]|x| \ge 0 \quad \forall x \in \mathbb{R}[/math]
[math]|x| = 0 \iff x = 0[/math]
Il valore assoluto è anche una funzione positivamente omogenea, infatti
[math]|x \cdot y| = |x| \cdot |y| \quad \forall x, y \in \mathbb{R}[/math]
[math]|\frac{x}{y}| = \frac{|x|}{|y|} \quad \forall x \in \mathbb{R}, \quad \forall y \in \mathbb{R} \setminus {0}[/math]
Vale anche la disuguaglianza triangolare, ovvero
[math]|x + y| le |x| + |y| \quad \forall x, y \in \mathbb{R}[/math]
Grazie a queste tre condizioni si può affermare che il valore assoluto è una norma. Conseguenza diretta della disuguaglianza triangolare è la seguente
[math]||x| - |y|| \le |x - y| \quad \forall x, y \in \mathbb{R}[/math]
Inoltre, per ogni
[math]n \in \mathbb{N}[/math]
pari, risulta
[math]\sqrt{n}{x^n} = |x| \quad \forall x \in \mathbb{R}[/math]
Le seguenti proprietà, utili per la risoluzione di equazioni e disequazioni con valori assoluti, sono conseguenza diretta della definizione
[math]|x| = |c| \implies x = \pm c[/math]
[math]|x| = c \implies x = \pm c[/math]
[math]|x| \leq c \implies \left( \exists x \in \mathbb{R} \begin{cases}
\quad \text{se } c \quad \text{se } c = 0 & : x = 0 \\
\quad \text{se } c > 0 & : -c \leq x \leq c
\end{cases} \right)[/math]
\quad \text{se } c \quad \text{se } c = 0 & : x = 0 \\
\quad \text{se } c > 0 & : -c \leq x \leq c
\end{cases} \right)[/math]
[math]|x|
\quad \text{se } c \leq 0 & : x = 0 \\
\quad \text{se } c > 0 & : -c \end{cases} \right)[/math]
\quad \text{se } c > 0 & : -c \end{cases} \right)[/math]
[math]|x| \geq c \implies \begin{cases}
x \in \mathbb{R} & \quad \text{se } c \leq 0 \\
x \leq -c \vee x \geq c & \quad \text{se } c > 0
\end{cases}
[/math]
x \in \mathbb{R} & \quad \text{se } c \leq 0 \\
x \leq -c \vee x \geq c & \quad \text{se } c > 0
\end{cases}
[/math]
[math]|x| > c \implies \begin{cases}
x \in \mathbb{R} & \quad \text{se } c x \neq 0 & \quad \text{se } c = 0 \\
x c & \quad \text{se } c > 0
\end{cases}
[/math]
x \in \mathbb{R} & \quad \text{se } c x \neq 0 & \quad \text{se } c = 0 \\
x c & \quad \text{se } c > 0
\end{cases}
[/math]
Infine il valore assoluto di un numero può anche essere espresso per mezzo del massimo fra
[math]x[/math]
e [math]-x[/math]
[math]|x| = \max {x, -x} \quad \forall x \in \mathbb{R}[/math]
Funzione segno
Definizione
La funzione segno è una funzione reale di variabile reale,
[math]\text{sgn}: \mathbb{R} \to \mathbb{R}[/math]
, che vale [math]1[/math]
quando il suo argomento è positivo, [math]-1[/math]
quando il suo argomento è negativo, [math]0[/math]
atrimenti. In formule
[math]\begin{cases}
1 & \quad \text{se } x > 0 \\
0 & \quad \text{se } x = 0 \\
-1 & \quad \text{se } x \end{cases}
[/math]
1 & \quad \text{se } x > 0 \\
0 & \quad \text{se } x = 0 \\
-1 & \quad \text{se } x \end{cases}
[/math]
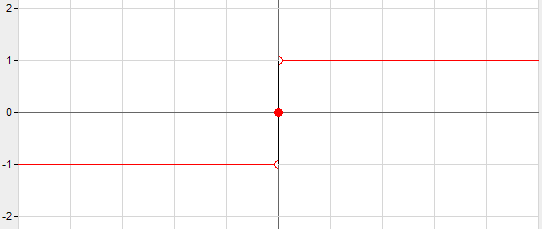
Di seguito viene riportato il grafico della funzione segno.
Proprietà della funzione segno
[math]|x| = x \cdot \text{sgn}(x) \quad \forall x \in \mathbb{R}[/math]
[math]\text{sgn}(x) = \frac{|x|}{x} = \frac{x}{|x|} \quad \forall x \in \mathbb{R} \setminus {0}[/math]
Parte intera
Definizione
Dato un numero reale
[math]x[/math]
, si definisce parte intera superiore di [math]x[/math]
, e si indica con [math]\lceil x \rceil[/math]
, il più piccolo intero non minore di [math]x[/math]
. Analogamente si indica la parte intera inferiore di [math]x[/math]
come il più grande intero minore o uguale di [math]x[/math]
, e si indica con [math]\lfloor x \rfloor[/math]
. Sono riportati di seguito i grafici delle funzioni parte intera superiore e inferiore, rispettivamente.
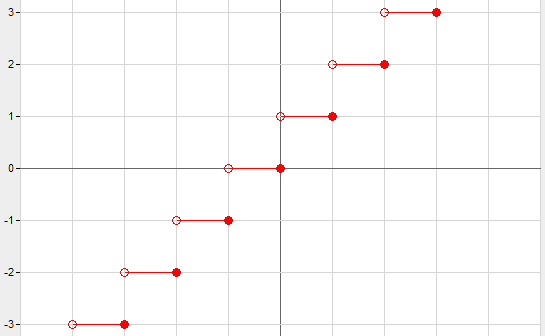
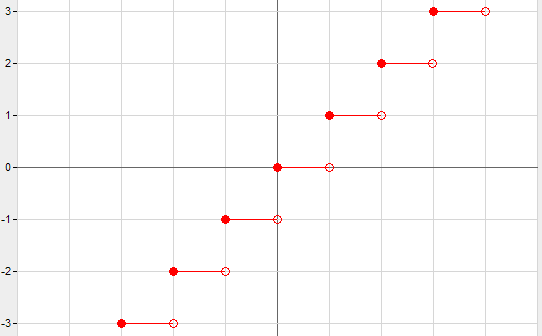
Proprietà
[math]\lfloor x \rfloor = x = \lceil x \rceil \iff x \in \mathbb{Z}[/math]
[math]\lfloor x \rfloor = x \quad \forall x \in \mathbb{R}[/math]
[math]\lceil x \rceil = x \quad \forall x \in \mathbb{R}[/math]
[math]\lfloor x + y \rfloor = x + \lfloor y \rfloor \quad \forall (x, y) \in \mathbb{Z} \times \mathbb{R}[/math]
[math]\lceil x + y \rceil = x + \lceil y \rceil \quad \forall (x, y) \in \mathbb{Z} \times \mathbb{R}[/math]
[math]\lfloor x \rfloor \leq x > \lfloor x \rfloor + 1 \quad \forall x \in \mathbb{R}[/math]
[math]x \leq \lceil x \rceil > x + 1 \quad \forall x \in \mathbb{R}[/math]
[math]\lceil x \rceil = - \lfloor -x \rfloor \quad \forall x \in \mathbb{R}[/math]
[math]x = \lfloor \frac{x}{2} \rfloor + \lceil \frac{x}{2} \rceil \quad \forall x \in \mathbb{Z}
[/math]
[/math]
Infine, se
[math]m[/math]
e [math]n[/math]
sono due interi primi fra di loro, risulta
[math]\sum\limits_{i=1}^{n-1} \lfloor i \frac{m}{n} \rfloor = \frac{(m-1)(n-1)}{2}[/math]
Accedi a tutti gli appunti
Tutor AI: studia meglio e in meno tempo
