Determina le soluzioni della seguente disequazione di secondo grado irrazionale:
Svolgimento
Per risolvere questa disequazione irrazionale, dobbiamo impostare un sistema a tre disequazioni in questo modo:
\begin{cases}
x - 1 > 0 \\
x^2 - 4x \;?\; 0 \\
(\sqrt{x^2 - 4x})^2 \end{cases}[/math]
Risolviamo le disequazioni:
1.
2.
Prendiamo come soluzioni gli intervalli esterni alle radici dell'equazione:
3.
Torniamo al sistema:
\begin{cases}
x > 1&\\
x \;?\; 0 \;?\; x \;?\; 4 \\
x > - \frac{1}{2} &
\end{cases}
[/math]
Determiniamo le soluzioni:


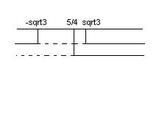






 Accedi a tutti gli appunti
Accedi a tutti gli appunti
 Tutor AI: studia meglio e in meno tempo
Tutor AI: studia meglio e in meno tempo