di francesco.speciale

Ominide

3 min. di lettura

Vota 4 / 5

[math]\sqrt{x+2}+\sqrt(x+4)>\sqrt(x-3)[/math]

;
Per l'esistenza della disequazione deve essere:

[math]\begin{cases} x+2>=0 \\ x+4>=0 \\ x-3>=0 \ \end{cases}[/math]

;

[math]\begin{cases} x>=-2 \\ x>=-4 \\ x>=3 \ \end{cases}[/math]

;
L'unione delle soluzioni sarà:

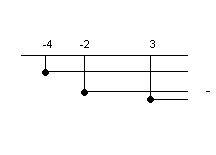
ovvero

[math]x>=3[/math]

.
In tale condizione i due membri sono positivi, elevando al quadrato si deve risolvere il sistema:

[math]\begin{cases} (\sqrt{x+2}+\sqrt(x+4))^2>(\sqrt(x-3))^2 \\ x>=3 \ \end{cases}[/math]

;

[math]\begin{cases} x+2+x+4+2\sqrt{(x+2)(x+4)}>x-3 \\ x>=3 \ \end{cases}[/math]

;
Semplificando

[math]\begin{cases} x+9+2\sqrt{(x+2)(x+4)}>0 \\ x>=3 \ \end{cases}[/math]

;

[math]\begin{cases} \sqrt{(x+2)(x+4)}>-(x+9)/2 \\ x>=3 \ \end{cases}[/math]

;

[math]\begin{cases} \sqrt{x^2+6x+8}>-(x+9)/2 \\ x>=3 \ \end{cases}[/math]

;

Risolviamo adesso l'equazione con un solo radicale, tenendo sempre presente la condizione

[math]x>=3[/math]

[math]\sqrt{x^2+6x+8}>-(x+9)/2[/math]

;
Essa è del tipo

[math]\sqrt{f(x)}>g(x)[/math]

quindi sarà equivalente al sistema:

[math]\begin{cases} f(x)>=0 \\ g(x)>0 \\ f(x)>[g(x)]^2 \ \end{cases}[/math]

;
Nel nostro caso

[math]f(x)=x^2+6x+8 ^^ g(x)=-(x+9)/2[/math]

.
Quindi la disequazione è equivalente al sistema:

[math]\begin{cases} x^2+6x+8>=0 \\ x^2+6x+8>(-(x+9)/2)^2 \\ -(x+9)/2>0 \ \end{cases}[/math]

;

[math]\begin{cases} x^2+6x+8>=0 \\ x^2+6x+8>(x^2+81+18x)/4 \\ -x>-9 \ \end{cases}[/math]

;

[math]\begin{cases} x^2+6x+8>=0 \\ 4x^2+24x+32>x^2+81+18x \\ x>9 \ \end{cases}[/math]

;

[math]\begin{cases} x^2+6x+8>=0 \\ 3x^2+6x-49>0 \\ x>9 \ \end{cases}[/math]

;
Studiamo separatamente le prime due disequazioni:

1)x^2+6x+8>=0

[math](Delta)/4=(b/2)^2-ac=(3)^2-(1 \cdot 8)=9-8=1[/math]

[math]x_(1,2)=(-b/2+-\sqrt{(Delta)/4})/a=(-3+-\sqrt1)=(-3+-1) => x_1=-4 ^^ x_2=-2[/math]

Siccome il segno del coefficiente di

[math]x^2[/math]

è concorde col segno della disequazione,
prenderemo gli intervalli esterni, quindi soluzione della disequazione sarà:

[math]x>=-4 vv x>=-2[/math]

2)3x^2+6x-49>0

[math](Delta)/4=(b/2)^2-ac=(3)^2-(3 \cdot (-49))=9+147=156[/math]

[math]x_(1,2)=(-b/2+-\sqrt{(Delta)/4})/a=(-3+-\sqrt(156))/3=(-3+-2\sqrt(39))/3 => x_1=(-3+2\sqrt(39))/3 ^^ x_2=(-3-2\sqrt(39))/3[/math]

Siccome il segno del coefficiente di

[math]x^2[/math]

è concorde col segno della disequazione,
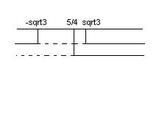
prenderemo gli intervalli esterni, quindi soluzione della disequazione sarà:

[math]x>(-3-2\sqrt{39})/3 vv x>(-3+2\sqrt{39})/3[/math]

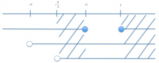
La soluzione del sistema si otiene considerando l'intersezione delle soluzioni delle singole disequazioni che lo conengono,
ricordando la condizione

[math]x>=3[/math]

Pertanto

[math]S={x>=3}[/math]

Disequazioni: sqrt(x+2)+sqrt(x+4)>sqrt(x-3)

sqrt(x+2)+sqrt(x+4)>sqrt(x-3) sqrt(x+2)+sqrt(x+4)>sqrt(x-3); Per l'esistenza della disequazione deve essere: {(x+2>=0),(x+4>=0),(x-3>=0):}; {(x>=-2),(x>=-4),(x>=3):}; L'unione delle soluzioni sarà : ovv

Recensioni

Domande e risposte

Help (321322)

Aiuto urgente per compiti

Problema con potenze

I migliori insegnanti di Matematica

Giovanni C.

Salvatore F.

Appunti correlati

Disequazioni: sqrt(x^2 - 1) < x + 3

Disequazioni: [math]\sqrt{{{x}^{2}+{2}}}-\sqrt{{{3}{x}-{1}}}>{4}{x}[/math]

Disequazioni: (sqrtx+sqrt(x-2)-1)/(sqrt(x^2+3)-sqrt(x+5)) ge 0

Disequazioni: sqrt(x^2-3)-sqrt(4x-5) lt=0

Recensioni

Domande e risposte

Help (321322)

Aiuto urgente per compiti

Problema con potenze

I migliori insegnanti di Matematica

Giovanni C.

Salvatore F.