Disequazioni: root(3)(x^3-3x^2)>=root(3)(-2x)

Ominide

1 min. di lettura

Vota

[math]root(3)(x^3-3x^2)>=root(3)(-2x)[/math]

Eleviamo ambo i membri al cubo

[math](root(3)(x^3-3x^2))^3>=(root(3)(-2x))^3[/math]

;

[math]x^3-3x^2>=-2x[/math]

;

[math]x^3-3x^2+2x>=0[/math]

;

[math]x(x^2-3x+2)>=0[/math]

Una prima soluzione sarà

[math]x>=0[/math]

.
Ora studiamo la disequazione d secondo grado:

[math]x^2-3x+2>=0[/math]

[math]Delta=b^2-4ac=(-3)^2-(4 \cdot 1 \cdot 2)=9-8=1[/math]

[math]x_(1,2)=(-b+-\sqrt{Delta})/(2a)=(3+-\sqrt1)/2=(3+-1)/2 => x_1=2 ^^ x_2=1[/math]

Siccome il segno del coefficiente di

[math]x^2[/math]

è concorde col segno della disequazione,
prenderemo gli intervalli esterni, quindi soluzione della disequazione sarà:

[math]x>=1 vv x>=2[/math]

Intersechiamo, ora, le soluzioni trovate e otterremo la soluzione finale

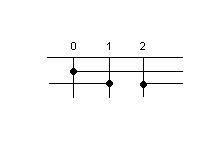
[math]S={0>=x>=1 vv x>=2}[/math]

Ti è piaciuto questo appunto?

root(3)(x^3-3x^2)>=root(3)(-2x) root(3)(x^3-3x^2)>=root(3)(-2x) Eleviamo ambo i membri al cubo (root(3)(x^3-3x^2))^3>=(root(3)(-2x))^3; x^3-3x^2>=-2x; x^3-3x^2+2x>=0; x(x^2-3x+2)>=0 Una prima...