Risolvi in
[math]RR[/math]
la seguente disequazione frazionaria
[math](x-2)/(x+2)-(x-3)/(x+3)>0[/math]
[math](x-2)/(x+2)-(x-3)/(x+3)>0[/math]
;
Il m.c.m. è
[math](x+2)(x+3)[/math]
, quindi
[math]((x-2)(x+3)-(x+2)(x-3))/((x+2)(x+3))>0[/math]
;
[math](x^2+3x-2x-6-(x^2+2x-3x-6))/((x+2)(x+3))>0[/math]
;
[math](x^2+3x-2x-6-x^2-2x+3x+6)/((x+2)(x+3))>0[/math]
;
Semplificando
[math](2x)/((x+2)(x+3))>0[/math]
;
Studiamo ora il numeratore e il denominatore
Numeratore
[math]2x>0 => x>0[/math]
.
Denominatore
[math](x+2)(x+3)>0[/math]
;
[math]x^2+5x+6>0[/math]
;
[math]Delta=b^2-4ac=(5)^2-(4 \cdot 1 \cdot 6)=25-24=1[/math]
[math]x_(1,2)=(-b+-\sqrt{Delta})/(2a)=(-5+-1)/2 => x_1=-2 ^^ x_2=-3[/math]
.
Siccome il coefficiente di
[math]x^2[/math]
e il segno della disequazione sono concordi,
prenderemo come soluzione accettabile l'intervallo esterno, per cui la soluzione sarà:
[math]x>-3 ^^ x> -2[/math]
.
Ora intersechiamo le soluzioni riguardanti il numeratore e il denominatore, ricavando così la soluzione della disequazione
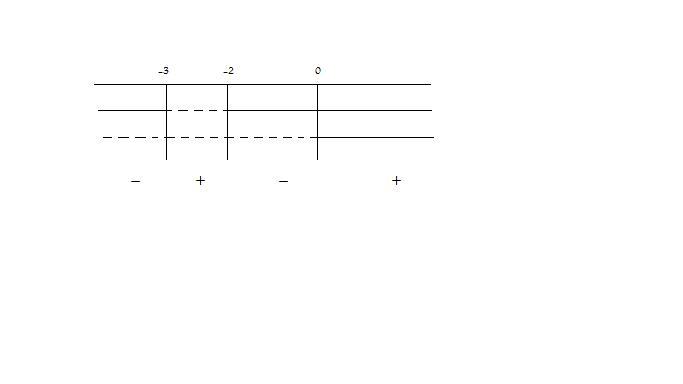
La soluzione sarà
[math]-3>x>-2 ^^ x>0[/math]
.
Accedi a tutti gli appunti
Tutor AI: studia meglio e in meno tempo
