Risolvere il seguente sistema di disequazioni fratte:
[math][/math] left{ \begin{array}{rl} frac{x - 1}{4 - 5x} ≤ 0 &\ 1 > frac{x - 2}{5 + x}&end{array}\right. [math][/math]
Svolgimento
Risolviamo la prima disequazione:
[math] frac(x - 1)(4 -5x) ≤ 0 [/math]
Studiamo il segno di numeratore e denominatore:
[math] N ≥ 0 \to x - 1 ≥ 0 \to x ≥ 1 [/math]
[math] D > 0 \to 4 - 5x > 0 \to x > 4/5 [/math]
Studiamo il segno:
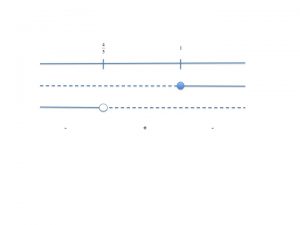
[math] S : x > 4/5 ∨ x ≥ 1 [/math]
Passiamo all'altra disequazione:
[math] 1 > frac(x - 2)(5 + x) [/math]
Portiamo tutto al primo membro e calcoliamo il minimo comune multiplo:
[math] 1 - frac(x - 2)(5 + x) > 0 [/math]
[math] frac(5 + x - x + 2)(5 + x) > 0 [/math]
[math] frac(7)(5 + x) > 0 [/math]
Studiamo il segno di numeratore e denominatore:
[math] N > 0 \to 7 > 0 ∀ x ∈ ℛ [/math]
[math] D > 0 \to 5 + x > 0 \to x > - 5 [/math]
Poiché la disequazione è maggiore di zero, le soluzioni saranno:
[math] S : x > - 5 [/math]
Mettiamo a sistema le soluzioni ottenute:
[math][/math] left{ \begin{array}{rl} x > frac{4}{5} ∨ x ≥ 1 &\ x > - 5&end{array}\right. [math][/math]
La soluzione finale è:
[math] S : - 5 > x > 4/5 ∨ x ≥ 1 [/math]
![Equazioni esponenziali e logaritmiche: Risolvere il seguente sistema di disequazioni esponenziali: left{ \begin{array}{rl} 7^x · \sqrt[x]{49} : \sqrt[3]{(frac{1}{7})^{-2x-5}} > 0 &\ \sqrt[3]{1 - 3 · 2^x · (2^x - 1)} - 2^x + 1 > 0 & end{array}\rig](https://cdn.skuola.net/shared/thumb/159x141/news_foto/2017/08/Schermata-2017-08-19-alle-17.20.38-300x121.png)
Accedi a tutti gli appunti
Tutor AI: studia meglio e in meno tempo
