[math]\frac{12}{35}[/math]
di un trapezio isoscele avente la base maggiore e la base minore rispettivamente uguali al triplo e alla metà del perimentro del quadrato.
Calcolare
- la misura della diagonale del quadrato;
- la lunghezza del perimetro del trapezio;
- l'area di un parallelogramma avente uno dei lati consecutivi uguale al lato del quadrato, l'altro ai [math]\frac{2}{3}[/math]dello stesso lato del quadrato e sapendo che i due lati consecutivi formano un angolo di 30°.
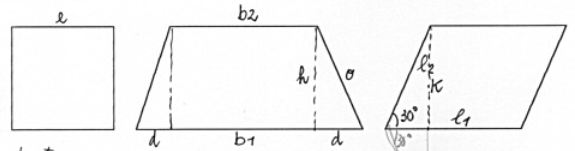
Soluzione
QuadratoPerimetro =
[math]48 cm[/math]
, da cui
[math]l = \frac{48}{4} cm = 12 cm[/math]
. La diagonale del quadrato è allora: diagonale =
[math]l \cdot \sqrt{2} = 12 \cdot \sqrt{2} cm[/math]
, cioè circa
[math]16,97 cm[/math]
.
Si ha poi che l'area del quadrato vale:
[math]A_q = l^2 = 144 cm^2[/math]
.
Trapezio isoscele
Base maggiore:
[math]b_1 = 3 \cdot 48 \text{perimetro quadrato} = 144[/math]
;
Base minore:
[math]b_2 = \frac{48}{2} = 24 cm[/math]
;
Area trapezio:
[math]A_t = \frac{35}{12} \cdot Aq = \frac{35}{12} \cdot 144 cm^2 = 420 cm^2[/math]
.
Nota che [math]\frac{35}{12}[/math] è il reciproco della frazione data.
Per il segmento abbiamo:
[math]d = (b_1 - b_2) / 2 = 120 / 2 = 60 cm[/math]
.
Per calcolare il lato obliquo del trapezio applichiamo il teorema di Pitagora:
[math] \theta = \sqrt{h^2+d^2} = \sqrt{25+360} \backsimeq 19.62 cm[/math]
.
Il perimetro del trapezio è dato da
[math]b_1 + b_2 + 2\theta[/math]
.
Parallelogramma
[math]l_1 = 12 cm[/math]
;
[math]l_2 = \frac{2}{3} \cdot 12 = 8 cm[/math]
.
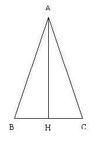
Per calcolare l'altezza
[math]k[/math]
del parallelogramma osserviamo che il triangolo a sinistra è metà di un triangolo equilatero.
[math]k = 1/2 l_2 = 4 cm[/math]
.
Area parallelogramma = base per altezza =
[math]12 \cdot 4 cm = 48 cm[/math]
.
Accedi a tutti gli appunti
Tutor AI: studia meglio e in meno tempo
