Soluzione

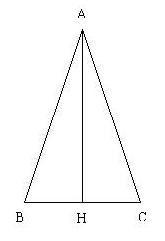
Dati:

[math]\bar{AH}=12cm[/math]

[math]\bar{BC}=6cm[/math]

[math]\bar{AB}=\bar{AC}[/math]

Svolgimento

Osserviamo che

[math]\bar{BH}=\frac{\bar{BC}}{2}=\frac{6}{2}cm=3cm[/math]

Applicando il Teorema di Pitagora al triangolo

[math]\hat{ABH}[/math]

si ha

[math]\bar{AB}=\sqrt{{\bar{AH}}^2+{\bar{BH}}^2}=\sqrt{{12cm}^2+{3cm}^2}=\sqrt{144+9}cm=\sqrt{153}cm=12,37cm[/math]

Il perimetro del triangolo isoscele allora sarà

[math]2p=\bar{AB}+\bar{AC}+\bar{BC}=(12,37+12,37+6)cm=30,74cm[/math]

Recensioni

3,3/5

3 recensioni

5 stelle

4 stelle

3 stelle

2 stelle

1 stella

Ti è piaciuto questo appunto?

Isoscele

scusi ma io cercavo tutto il problema, ma io non dicevo tutto tutto ma solo i dati e il calcolo punto

19 Dicembre 2014

Omar Compleanno

il problema era facile l'ho risolto insieme alla mia classe "quasi" tutti l'hanno capito tranne qualcuno el.....

16 Aprile 2014

Mary

Devo dire che ci sono degli esercizi molto semplici ma anche con difficile diffcoltà.Nostante tutto ci sono esercizi che mi sarebbe piaciuto svolgere,ma c'è già la solzione: io pensavo fossero da fare ma meglio così perchè spiegando le cose come vanno fatte,il lettore può capire dove sbaglia in alcuni problemi simili ho comunque nell'applicare una certa formula.

18 Agosto 2012

Domande e risposte

Hai bisogno di aiuto?

Chiedi alla community

Fai una domanda

Problemi di II media: Calcola il perimetro di un triangolo isoscele hat{ABC}, sapendo che l'altezza è lunga 12cm

Esercizio di geometria sul triangolo isoscele. Si chiede di calcolare il perimetro conoscendo l'altezza e la base.