Il rettangolo
[math]ABCD[/math]
ha il perimetro ed il lato
[math]AB[/math]
lunghi rispettivamente
[math]268 cm[/math]
e
[math]6 dm[/math]
. Sul lato
[math]DC[/math]
si è preso il punto
[math]P[/math]
tale che la misura del segmento
[math]DP[/math]
superi quella di
[math]PC[/math]
di
[math]52 cm[/math]
, e si è congiunto
[math]P[/math]
con
[math]A[/math]
e
[math]B[/math]
.
Calcola l'area e la misura del perimetro di ciascuno dei tre triangoli in cui il rettangolo è diviso.
Soluzione
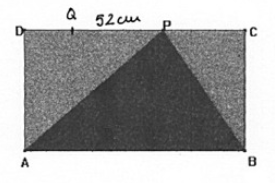Il segmento [math]DP[/math]
si compone di due parti:
[math]DQ = PC[/math]
e
[math]QP = 52 cm[/math]
.
Poiché
[math]\bar(AB) = \bar(DC) = 60 cm[/math]
, sottraendo
[math]52 cm[/math]
otteniamo
[math]8 cm[/math]
, che è la misura di
[math]\bar(DQ)[/math]
e
[math]\bar(PC)[/math]
insieme.
Quindi
[math]\bar(PC) = 4 cm[/math]
,
[math]\bar(DP)=56 cm[/math]
.
Per calcolare
[math]\bar(DA)[/math]
dividiamo per due il perimetro e sottriamo
[math]\bar(AB)[/math]
:
[math]\bar(DA) = 134 cm - 60 cm = 74 cm[/math]
.
Per calcolare
[math]\bar(AP)[/math]
applichiamo il teorema di Pitagora al triangolo
[math]ADP[/math]
.
Per calcolare
[math]\bar(PB)[/math]
applichiamo il teorema di Pitagora al triangolo
[math]PCB[/math]
.
Con queste informazioni possiamo calcolare i perimetri dei tre triangoli.
Abbiamo infine:
[math]text(Area(ADP)) = (\bar(AD)cdot \bar(DP))/2[/math]
[math]text(Area(PCB))= (\bar(PC)cdot \bar(CB))/2[/math]
[math]text(Area(APB))= text(Area ret\\tangolo) - text(Area(ADP)) - text(Area(PCB))[/math]
Accedi a tutti gli appunti
Tutor AI: studia meglio e in meno tempo
