Termologia: Un pezzo di metallo di massa  100 g  ha una temperatura di  150 °C . Dopo essere stato immerso in  50 g  di acqua, che si trovava inizialmente alla temperatura di  20 °C ...

Calcolare il calore specifico di un metallo conoscendo la temperatura di equilibrio raggiunta dal sistema costituito da acqua e metallo

_francesca.ricci
di _francesca.ricci
Ominide
2 min. di lettura
Vota

Concetti Chiave

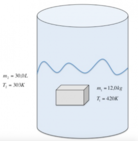
  • Un pezzo di metallo da 100 g viene immerso in 50 g di acqua, equilibrando le temperature da 150°C e 20°C a 40°C.
  • Le masse sono convertite in chilogrammi: 100 g = 0,1 kg e 50 g = 0,05 kg, mentre le temperature sono convertite in Kelvin.
  • La condizione di equilibrio termico implica che la somma delle energie scambiate tra metallo e acqua sia nulla.
  • La formula per l'energia scambiata è Q = cmΔT, dove ΔT è la differenza tra la temperatura finale e quella iniziale.
  • Il calore specifico del metallo viene calcolato come 380,5 J/(kg·K), approssimato a 3,0 x 10² J/(kg·K).

Un pezzo di metallo di massa

[math]100 g[/math]
ha una temperatura di
[math]150 C[/math]
. Dopo essere stato immerso in
[math]50 g[/math]
di acqua, che si trovava inizialmente alla temperatura di
[math]20 C[/math]
, il metallo e lacqua raggiungono una temperatura di equilibrio di
[math]40 C[/math]
.
  • Qual il calore specifico del metallo?

Svolgimento

Analizziamo i dati che abbiamo e trasformiamoli nelle giuste unit di misura:

[math] m_1 = 100 g = 100 \cdot 10^{-3} kg [/math]

[math] m_2 = 50 g = 50 \cdot 10^{-3} kg [/math]

[math]t_1 = 150C = 150 + 273,15 = 423,15 K [/math]

[math] t_2 = 20C = 20 + 273,15 = 293,15 K [/math]

Sappiamo inoltre che:

[math] c_a = 4186 frac(J)(kg \cdot K) , t_e = 40C = 40 + 273,15 = 313,15 K [/math]

Affinch vi sia equilibrio termico necessario che non vi siano scambi di energia fra le masse in

questione, cio che la somma dellenergia scambiata dallacqua e quella scambiata dallalluminio sia nulla, cio:

[math] Q_1 + Q_2 = 0 [/math]

Sappiamo che lenergia scambiata data dalla formula:

[math] Q = cm ?T [/math]

quindi:

[math] c_1 m_1 ?T_1 + c_2 m_2 ?T_2 = 0 [/math]

[math] ?T[/math]
la variazione di temperatura, cio la temperatura finale meno quella iniziale.

[math] ?T = T_f - T_i [/math]

Abbiamo la temperatura iniziale di entrambi i materiali, e anche quella finale, rappresentata dalla temperatura di equilibrio.

[math] c_1 m_1 (T_e - T_(i_1))_1 + c_2 m_2 (T_e - T_(i_2))_2 = 0 [/math]

Ricaviamo dalla formula il calore specifico del metallo:

[math] c_1 m_1 (T_e - T_(i_1))_1 = - c_2 m_2 (T_e - T_(i_2))_2 [/math]

[math] c_1 = - frac(c_2 m_2 (T_e - T_(i_2))_2)(m_1 (T_e - T_(i_1))_1) [/math]

Sostituiamo i dati e ricaviamo il valore del calore specifico:

[math] c_1 = - frac(4186 \cdot 50 \cdot 10^{-3} \cdot (313,15 - 293,15))( 100 \cdot 10^{-3} (313,15 - 423,15)) = [/math]

[math] - frac(4186 \cdot 50 \cdot 10^{-3} \cdot 20)( 100 \cdot 10^{-3} (- 100)) = 380,5 frac(J)(kg \cdot K) = 3,0 \cdot 10^2 frac(J)(kg \cdot K) [/math]

Domande da interrogazione

  1. Qual è la formula utilizzata per calcolare il calore specifico del metallo?

    2. La formula utilizzata è [math] c_1 = - \frac{c_2 m_2 (T_e - T_{i_2})}{m_1 (T_e - T_{i_1})} [/math], dove [math] c_2 [/math] è il calore specifico dell'acqua, [math] m_1 [/math] e [math] m_2 [/math] sono le masse del metallo e dell'acqua, e [math] T_e [/math], [math] T_{i_1} [/math], [math] T_{i_2} [/math] sono le temperature di equilibrio e iniziali.

  2. Quali sono le temperature iniziali e di equilibrio utilizzate nel calcolo?

    3. Le temperature iniziali sono [math] 150 C [/math] per il metallo e [math] 20 C [/math] per l'acqua, mentre la temperatura di equilibrio è [math] 40 C [/math].

  3. Qual è il valore del calore specifico del metallo calcolato?

    4. Il calore specifico del metallo calcolato è [math] 380,5 \frac{J}{kg \cdot K} [/math], approssimato a [math] 3,0 \cdot 10^2 \frac{J}{kg \cdot K} [/math].

Appunti correlati

Domande e risposte

Hai bisogno di aiuto?
Chiedi alla community
Fai una domanda

Aiuto per Errori per Fisica
_francesca.ricci di Linustrike

aiuto studio
_francesca.ricci di Giorgia.obe

Esercizi con i vettori
_francesca.ricci di DAMIANO2011

I migliori insegnanti di Fisica

Salvatore

Salvatore F.

Supertutor
Percorsi
Verificato
DSA

Insegnante di Aiuto compiti, Aiuto tesi, Algebra, Analisi 1

a partire da 20 €/ora
most booked
Matteo

Matteo S.

Supertutor
Verificato

Insegnante di Aiuto tesi, Algebra, Geometria, Matematica

a partire da 20 €/ora
most booked
Mostra altri Tutor