Termologia: Un gas perfetto contiene 10,35 * 10^23 molecole.... (esercizi termodinamica)

Esercizi di termodinamica: applicazione della legge dei gas perfetti e della legge di Boyle

_francesca.ricci
di _francesca.ricci
Ominide
4 min. di lettura
Vota

Concetti Chiave

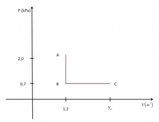
  • Il gas perfetto subisce una trasformazione ciclica con due isoterme (BC e DA) e due isobare (AB e CD).
  • Le temperature delle trasformazioni isoterme sono calcolate utilizzando l'equazione di stato dei gas perfetti e la costante di Boltzmann.
  • La temperatura nel tratto BC è calcolata come 72,6 K, mentre nel tratto DA è di 11,1 K.
  • I volumi negli stati A e C sono determinati usando la legge di Boyle, con valori di 6,83 x 10^-3 m^3 e 6,32 x 10^-4 m^3 rispettivamente.
  • Le trasformazioni cicliche coinvolgono variazioni di pressione e volume, mentre la temperatura rimane costante nelle isoterme.
Un gas perfetto contiene
[math]10,35 \cdot 10^23[/math]
molecole ed è sottoposto a un trasformazione ciclica composta da due isoterme (BC e DA) e da due isobare (AB e CD) come nella figura.

I valori del volume e della pressione negli stati B e D sono:

[math]V_B = 4,15 dm^3 , V_D = 1,04 dm^3 [/math]

[math]p_B = 2,50 \cdot 10^5 Pa , p_D = 1,52 \cdot 10^5 Pa [/math]

  • Calcola il valore delle temperature
    [math]T_1[/math]
    e
    [math]T_2[/math]
    a cui avvengono le due trasformazioni isoterme.
  • Calcola il valore del volume negli stati A e C della trasformazione.

Quesito 1

Per prima cosa, trasformiamo i valori del volume nella giusta unità di misura:

[math]V_B = 4,15 dm^3 = 4,15 \cdot 10^{-3} m^3[/math]

[math] V_D = 1,04 dm^3 = 1,04 \cdot 10^{-3} m^3[/math]

Per calcolare la temperatura nei tratti in cui avviene la trasformazione isoterma consideriamo l'equazione di stato dei gas perfetti:

[math]pV = nRT[/math]

dove n è il numero di moli.

Poiché noi abbiamo il numero di molecole possiamo sfruttare la formula

[math] n = frac(N)(N_A) [/math]

dove

[math]N_A[/math]

è il numero di Avogadro.

Sostituiamo questa formula all'equazione di stato dei gas perfetti:

[math]pV = frac(N)(N_A) RT[/math]

Notiamo che la formula può essere scritta anche in questo modo:

[math]pV = N frac(R)(N_A) T[/math]

Abbiamo quindi un quoziente fra due costanti:

[math]frac(R)(N_A)[/math]

che corrisponde alla costante di Boltzmann (

[math]k_B = 1,38 \cdot 10^{-23} J/K [/math]

):

[math]pV = N k_B T[/math]

Sostituiamo la pressione e il volume nel punto B per calcolare la temperatura a cui avviene la trasformazione nel tratto BC:

[math]p_B V_B = N k_B T_(BC) \to T_(BC) = frac(p_B V_B)(N k_B)[/math]

Quindi abbiamo:

[math]T_(BC) = frac(2,50 \cdot 10^5 Pa \cdot 4,15 \cdot 10^{-3} m^3 )(10,35 \cdot 10^23 \cdot 1,38 \cdot 10^{-23} J/K) = 72,6 K[/math]

Allo stesso modo calcoliamo la temperature nel tratto DA:

[math]p_D V_D = N k_B T_(DA) \to T_(DA) = frac(p_D V_D)(N k_B)[/math]

[math]T_(BC) = frac(1,52 \cdot 10^5 Pa \cdot 1,04 \cdot 10^{-3} m^3 )(10,35 \cdot 10^23 \cdot 1,38 \cdot 10^{-23} J/K) = 11,1 K[/math]

Quesito 2

Per calcolare il volume negli stati A e C consideriamo che le trasformazioni nei tratti BC e AD sono isoterme, cioè a temperatura costante.

Possiamo quindi utilizzare la legge di Boyle:

[math]p_0 V_0 = pV \to V = frac(p_0 V_0)(p)[/math]

Quindi:

[math] V_C = frac(p_B V_B)(p_C)[/math]

Poiché nel tratto CD la pressione è costante, la pressione nello stato c è uguale a quella nello stato D.

[math] V_C = frac(2,50 \cdot 10^5 Pa \cdot 4,15 \cdot 10^{-3} m^3)(1,52 \cdot 10^5 Pa) = 6,83 \cdot 10^{-3} m^3[/math]

Allo stesso modo calcoliamo il volume nello stato A, tenendo presente che la pressione in quello stato è uguale a quella nel punto B:

[math] V_A = frac(p_D V_D)(p_A)[/math]

[math] V_A = frac(1,52 \cdot 10^5 Pa \cdot 1,04 \cdot 10^{-3} m^3)(2,50 \cdot 10^5 Pa) = 6,32 \cdot 10^{-4} m^3[/math]

Domande da interrogazione

  1. Come si calcolano le temperature delle trasformazioni isoterme nel ciclo del gas perfetto?

    2. Le temperature delle trasformazioni isoterme si calcolano utilizzando l'equazione di stato dei gas perfetti, [math]pV = Nk_BT[/math], sostituendo i valori di pressione e volume nei punti specifici del ciclo.

  2. Qual è la temperatura nel tratto BC della trasformazione isoterma?

    3. La temperatura nel tratto BC è calcolata come [math]T_{BC} = \frac{p_B V_B}{N k_B}[/math], risultando in 72,6 K.

  3. Come si determina il volume negli stati A e C della trasformazione?

    4. Il volume negli stati A e C si determina utilizzando la legge di Boyle, [math]p_0 V_0 = pV[/math], considerando che le trasformazioni BC e AD sono isoterme.

  4. Qual è il volume nello stato C?

    5. Il volume nello stato C è calcolato come [math]V_C = \frac{p_B V_B}{p_C}[/math], risultando in [math]6,83 \cdot 10^{-3} m^3[/math].

Appunti correlati

Domande e risposte

Hai bisogno di aiuto?
Chiedi alla community
Fai una domanda

Aiuto per Errori per Fisica
_francesca.ricci di Linustrike

aiuto studio
_francesca.ricci di Giorgia.obe

Esercizi con i vettori
_francesca.ricci di DAMIANO2011

I migliori insegnanti di Fisica

Salvatore

Salvatore F.

Supertutor
Percorsi
Verificato
DSA

Insegnante di Aiuto compiti, Aiuto tesi, Algebra, Analisi 1

a partire da 20 €/ora
most booked
Matteo

Matteo S.

Supertutor
Verificato

Insegnante di Aiuto tesi, Algebra, Geometria, Matematica

a partire da 20 €/ora
most booked
Mostra altri Tutor