Concetti Chiave
- Il documento esplora le vibrazioni libere nei sistemi meccanici ed elettrici attraverso equazioni differenziali del secondo ordine lineari omogenee a coefficienti costanti.
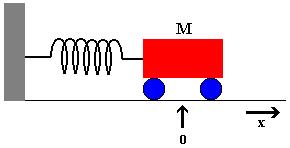
- Il sistema meccanico analizzato include un carrello di massa M collegato a una molla con attrito viscoso, descritto da un'equazione differenziale specifica.
- Viene fornita sia una soluzione simbolica esatta che un'approssimazione per l'equazione del sistema meccanico, con indicazioni su variabili temporali e passi temporali.
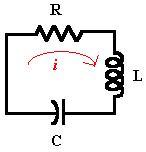
- Il circuito elettrico considerato comprende resistenza, induttanza e condensatore, modellato da un'equazione differenziale che descrive la variazione di carica (Q).
- Anche per il sistema elettrico, vengono presentate soluzioni simboliche esatte e approssimate, con dettagli sui parametri temporali.
In questo file illustreremo le vibrazioni libere in sistemi meccanici e in sistemi elettrici rappresentate da equazioni differenziali del secondo ordine lineari omogenee con coefficienti costanti.
Consideriamo un carrello di massa M, collegato ad una molla che esercita una forza, proporzionale alla distanza dal centro di oscillazione, uguale a
, con attrito viscoso del mezzo espresso da una forza del tipo 
. 
Questa è l'immagine del carrello nella posizione di equilibrio ( x = 0).
L'equazione differenziale per questo sistema meccanico è:
per 
Immettiamo i valori dei coefficienti:
Trasformazione nella forma standard:
at 
La soluzione simbolica esatta viene riportata qui sotto.
Soluzione simbolica :
Soluzione approssimata :
estremo destro temporale variabile
numero di passi temporali
Consideriamo un semplice circuito elettrico contenente una resistenza, una induttanza e un condensatore. La variazione di Q sulle superfici del condensatore è rappresentata dalla seguente equazione differenziale:
at 
Immettiamo i valori dei coefficienti:
Trasformazione nella forma standard:
at 
La soluzione simbolica esatta viene riportata qui sotto.
Soluzione simbolica :
Soluzione approssimata:
numero di passi temporali
estremo destro temporale variabile
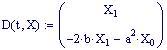
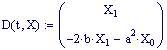
Accedi a tutti gli appunti
Tutor AI: studia meglio e in meno tempo
