Concetti Chiave
- Il moto del pendolo smorzato è descritto da un sistema di equazioni che includono posizione e velocità angolare, con smorzamento costante.
- Le soluzioni numeriche sono calcolate utilizzando il metodo Runge-Kutta del quarto ordine, con passo temporale fisso e condizioni iniziali specifiche.
- Otto soluzioni vengono generate e tracciate, con vettori derivativi che calcolano le derivate di posizione e velocità per blocchi.
- Il tracciato di fase mostra direzioni di evoluzione delle soluzioni attraverso frecce, con spaziatura ogni quindicesimo punto.
- Tre punti di equilibrio sono visibili nel tracciato: due stabili e uno instabile, con traiettorie che si avvicinano o spiraleggiano verso questi punti.
Il Pendolo Smorzato
Questi appunti mostrano le varie fasi per la costruzione del il sistema di equazioni che descrivono il moto di un pendolo smorzato a partire dalle:
Condizioni iniziali relative alla posizione e alla velocità
N , il numero di passi da rilevare lungo l'intervallo temporale
c , la costante di smorzamento
Ambiente
Le equazioni del moto di un pendolo smorzato sono
dove p(t) è la posizione angolare del pendolo e v(t) è la velocità angolare.
E' possibile costruire soluzioni sull'intervallo temporale [0,20] per una serie di condizioni iniziali , usando una tecnica numerica detta
metodo del quarto ordine Runge–Kutta con passi di misura fissa.
Dapprima si sceglie un numero di passi e si definiscono variabili di escursione per generare le soluzioni:
numero di passi
dimensione del passo temporale
Variabili di escursione per generare e tracciare soluzioni:
Per generare otto soluzioni, conviene calcolarle a blocchi. Bisogna definire un vettore derivativo che dia le derivate di p e v per quattro soluzioni. Si verranno ad aggiungere altre righe alla matrice risolutiva. La costante di smorzamento c viene posta uguale a 0.2 .
blocco vettore derivativo
Condizioni iniziali
Ora si scelgono otto condizioni iniziali. In questo esempio , alcune traiettorie vengono fatte partire dalla posizione 0 con velocità positiva, e altre dalla posizione 2 p con una velocità negativa:
Integrazione numerica Runge–Kutta
Queste equazioni sviluppano l'approssimazione del passo Runge–Kutta che generera le traiettorie seguenti:
Le due seguenti equazioni definiscono iterazioni sull'indice i per generare le otto traiettorie . Per facilità di manipolazione, le condizioni iniziali vengono riunite in un sola matrice x . La colonna i-sima di x contiene le otto soluzioni , con le posizioni negli elementi pari e le velocità negli elementi dispari.
Indicare la direzione
Nell'interpretazione di un tracciato di fase è utile sapere la direzione e il verso secondo cui evolve ogni soluzione. Da solo, il grafico della soluzione non da questa informazione, ma può essere aggiunta posizionando frecce lungo la traiettoria che indichino la direzione corrispondente al variare del tempo. Le seguenti definizioni (alquanto complicate) hanno lo scopo di creare uno spazio ogni quindicesima colonna di x e di inserire punti che disegneranno le frecce.
La funzione seguente genera un vettore unitario nella direzione della freccia, che è la direzione del vettore che unisce il punto precedente al successivo. La variabile indipendente a questa funzione sarà una schiere due per due dove la prima fila denota le posizioni e la seconda le velocità per una soluzione particolare.
Porre la spaziatura delle frecce:
frecce ogni quindicesimo punto
Ora ricopiare x in X , lasciando spazi ogni K esima colonna per le frecce
Calcola i punti terminali delle frecce ed inseriscile in X . Il parametro di scala stabilisce la dimensione delle frecce.
Ripetere i punti sulle teste delle frecce, in modo che i lati si ripieghino sul punto:
Per tracciare i grafici, è necessaria una variabile di campo che che tenga conto dei punti in più aggiunti dalle frecce:
Ecco rappresentato lo spazio delle fasi completo, con la posizione angolare sull'asse orizzontale e la velocità angolare sull'asse verticale.
Tre punti di equilibrio, segnati da rettangoli neri, sono visibili in questo tracciato: due punti di equilibrio stabile in (0, 0) e (2 p , 0) , e un punto di equilibrio instabile in ( p , 0) .
Tutte le traiettorie tratteggiate in rosso hanno (0, 0) come loro limite: esse giacciono nel bacino di attrazione di questo punto di equilibrio. Le traiettorie blu, a linea continua, alla fine girano in spirale verso il prossimo equilibrio in (2 p , 0) . L'equilibrio instabile in ( p , 0) rappresenta uno stato dove il pendolo è senza moto ma la massa pendolare è all' inizio del ciclo. Quattro delle traiettorie si avvicinano molto a questo punto. In due di queste il pendolo raggiunge quasi la cima e poi cambia la direzione e ricade; per le altre due il pendolo ce la fa appena a superare la cima cadendo poi nella regione successiva del dominio angolare. Si può vedere dall'assembramento delle frecce vicino all'equilibrio instabile quale posizione e quale velocità sta cambiando lentamente in questa regione dello spazio delle fasi.
Domande da interrogazione
- Qual è il metodo utilizzato per risolvere le equazioni del moto del pendolo smorzato?
- Quali sono le condizioni iniziali considerate per le traiettorie del pendolo?
- Come viene rappresentata la direzione delle soluzioni nel tracciato di fase?
- Quali sono i punti di equilibrio nel tracciato di fase del pendolo smorzato?
- Come si comportano le traiettorie rispetto ai punti di equilibrio?
Il metodo utilizzato è il metodo del quarto ordine Runge-Kutta con passi di misura fissa.
Sono considerate otto condizioni iniziali, alcune con posizione iniziale 0 e velocità positiva, altre con posizione 2π e velocità negativa.
La direzione delle soluzioni è indicata posizionando frecce lungo la traiettoria, che mostrano la direzione del vettore che unisce il punto precedente al successivo.
Ci sono tre punti di equilibrio: due stabili in (0, 0) e (2π, 0), e uno instabile in (π, 0).
Le traiettorie tratteggiate in rosso convergono verso (0, 0), mentre quelle blu spiraleggiano verso (2π, 0). Alcune traiettorie si avvicinano al punto di equilibrio instabile (π, 0) ma poi cambiano direzione.

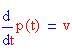
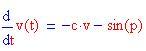
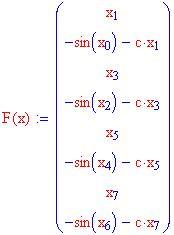
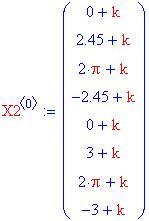
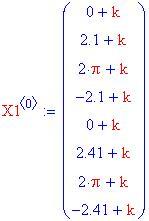
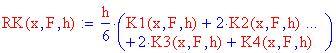
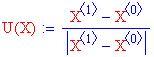
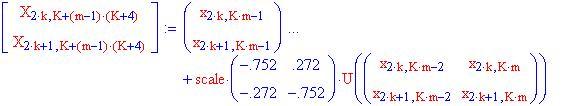
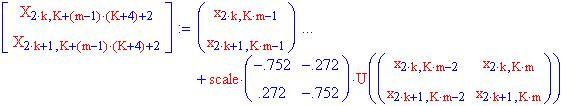
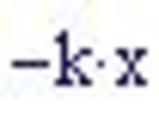





 Accedi a tutti gli appunti
Accedi a tutti gli appunti
 Tutor AI: studia meglio e in meno tempo
Tutor AI: studia meglio e in meno tempo