Concetti Chiave
- I moduli dei vettori \(\vec{a}\) e \(\vec{b}\) sono rispettivamente 5,0 e 8,0 unità.
- Il vettore \(\vec{c} = \vec{a} \cdot \vec{b}\) ha un modulo di 20 unità.
- Per calcolare l'angolo tra \(\vec{a}\) e \(\vec{b}\), si utilizza la formula \(\sin(\alpha) = \frac{c}{ab}\).
- Il seno dell'angolo \(\alpha\) è \(\frac{1}{2}\), corrispondente a un angolo di 30°.
- Il vettore \(\vec{d} = \vec{b} \cdot \vec{a}\) ha lo stesso modulo ma direzione opposta rispetto a \(\vec{c}\) a causa della proprietà anticommutativa.
In questo appunto imparerai a calcolare l'angolo compreso tra due vettori, oltre a ricordare alcune proprietà fondamentali del calcolo vettoriale e, in particolare, del prodotto vettoriale.
Testo dell'esercizio
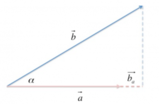
I due vettori
e
hanno modulo rispettivamente di
e
unità. Il vettore
ha modulo pari a
unità.
- Calcola l'ampiezza dell'angolo acuto formato dalle direzioni dei due vettori [math]\vec{a}[/math]e[math]\vec{b}[/math].
- Il vettore [math]\vec{d} = \vec{b} \times \vec{a}[/math]ha lo stesso modulo di[math]\vec{c}[/math]?
Svolgimento (1)
Possiamo calcolare il modulo del vettore risultante dal prodotto vettoriale di altri due vettori con la formula
Di conseguenza, se vogliamo calcolare l'ampiezza dell'angolo formato dai due vettori, ricaviamo il seno dell'angolo dalla formula precedente, chiamando per comodità di notazione
.
Quindi:
Dalla goniometria, sappiamo che se il seno di un angolo è uguale ad
, l'angolo ha un'ampiezza di
.
Altrimenti, possiamo calcolare, con la calcolatrice, l'angolo a cui corrisponde il seno noto:
Svolgimento (2)
Il vettore
ha lo stesso modulo e la stessa direzione del vettore
, poiché è dato dalla stessa formula; tuttavia, questo vettore avrà verso opposto, infatti vale la proprietà anticommutativa:
In sintesi, si conserva la direzione e il modulo, ma non il verso!
Accedi a tutti gli appunti
Tutor AI: studia meglio e in meno tempo
