Concetti Chiave
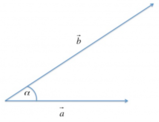
- I vettori \(\vec{a}\) e \(\vec{b}\) hanno moduli rispettivamente di 5,0 e 8,0 unità.
- Il prodotto scalare dei due vettori è dato come \(20 \sqrt{2}\).
- Il coseno dell'angolo tra i due vettori è calcolato come \(\frac{\sqrt{2}}{2}\).
- Utilizzando la formula del prodotto scalare, si ottiene che \(\cos(\alpha) = \frac{\vec{a} \cdot \vec{b}}{ab}\).
- L'angolo tra i due vettori è di 45°, dato che \(\cos(45°) = \frac{\sqrt{2}}{2}\).
In questo appunto rivedremo alcune delle proprietà del prodotto scalare.
Testo dell'esercizio
Due vettori[math]\vec{a}[/math]
e [math]\vec{b}[/math]
hanno moduli, rispettivamente, di [math]5,0[/math]
e [math]8,0[/math]
unità. Il valore del loro prodotto scalare è [math]20 \sqrt2[/math]
.Calcola l'ampiezza dell'angolo formato dalle direzioni dei due vettori.
Svolgimento dell'esercizio
Sapendo che il prodotto scalare dei due vettori è ,[math]20 \sqrt2[/math]
possiamo scrivere che:[math] \vec{a} \cdot \vec{b} = 20 \sqrt2 [/math]
[math]a, b[/math]
i moduli dei vettori [math]\vec{a}, \vec{b}[/math]
rispettivamente, ricordiamo che il prodotto scalare di due vettori si calcola anche con la formula[math] \vec{a} \cdot \vec{b} = = ab \cdot \cos(\alpha) [/math]
[math] \cos(\alpha) = \frac{\vec{a} \cdot \vec{b}}{ab} [/math]
[math] \cos(\alpha) = \frac{20 \sqrt2}{5,0 \cdot 8,0} = \frac{\sqrt2}{2} [/math]
[math]\frac{\sqrt{2}}{2} [/math]
, l'angolo ha ampiezza pari a 45 gradi.Altrimenti, possiamo calcolare, con la calcolatrice, l'angolo a cui corrisponde il seno noto utilizzando la funzione inversa del coseno, cioè l'arcocoseno.
Domande da interrogazione
- Qual è la formula per calcolare il prodotto scalare di due vettori?
Il prodotto scalare di due vettori \(\vec{a}\) e \(\vec{b}\) si calcola con la formula \(\vec{a} \cdot \vec{b} = ab \cdot \cos(\alpha)\), dove \(a\) e \(b\) sono i moduli dei vettori e \(\alpha\) è l'angolo tra di essi.
Accedi a tutti gli appunti
Tutor AI: studia meglio e in meno tempo
