Concetti Chiave
- La rappresentazione di fenomeni su scala ridotta è necessaria per visualizzarli comodamente, come nel caso dei planisferi.
- Le riduzioni in scala permettono di rappresentare grandezze enormi o minuscole in modo proporzionale e comprensibile su supporti più piccoli.
- Un esempio pratico di riduzione in scala si trova nel calcolo delle velocità, dove un segmento di carta rappresenta una velocità reale.
- Per una scala data, un segmento di 5 cm rappresenta 20 km/h; utilizzando una proporzione, si può calcolare la lunghezza per altre velocità.
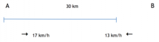
- Nel problema proposto, un segmento di 7,5 cm rappresenta una velocità di 30 km/h, mantenendo la proporzionalità della scala.
Come è noto, è sempre difficile rappresentare un fenomeno su una scala reale, proprio perché le dimensioni (a volte troppo piccole, a volte troppo grandi) non consentono una visualizzazione umanamente "comoda".
Per questo a volte è necessario ridurre in scala determinate cose nella loro rappresentazione. In effetti, basti pensare per esempio ai planisferi: è chiaramente impossibile rappresentare tutto il mondo su un foglio di carta, eppure ce la si fa dicendo che una certa misura sulla carta corrisponde ad una misura ben definita nella realtà.
Ovviamente, all'aumentare della misura sulla carta aumenta (linearmente) la misura del pezzo corrispondente nella realtà, in maniera proporzionale.
Queste riduzioni possono tornare utili anche in fisica; vediamo un esempio.
Testo dell'esercizio
Se, fissata una scala, una velocità di modulo
Soluzione dell'esercizio
La scala fa corrispondereImpostiamo la proporzione:
Accedi a tutti gli appunti
Tutor AI: studia meglio e in meno tempo
